Molecular dynamics simulation of unfolding of histidine-containing
phosphocarrier protein in water
Atsushi SUENAGA, Yuto KOMEIJI, Masami UEBAYASI,
Toshiyuki MEGURO, and Ichiro YAMATO
 Return
Return
I. INTRODUCTION
The theoretical study of the process of protein unfolding provides some insights into the mechanism of protein folding, which remains an important subject in molecular biology. Recently, it has been reported that several proteins can exist in partially structured states which are stable under certain conditions [1 ~ 5]. Such structures are known to be in 'molten globule states'. In a molten globule state, a structure appears to be compact, to be mobile and to retain secondary structure but not native tertiary structure [4]. Although the structural details of the native, folded conformation of proteins have been determined, those of the intermediates of folding/unfolding are difficult to characterize by experiments due to large fluctuations and the lack of a fixed structure throughout the molecules [6 ~ 10].
Molecular dynamics (MD) simulation is useful for understanding protein structures and dynamical properties. In principle, MD can reveal the details of the intermediate structures and dynamic transitions that occur during the unfolding process. For these reasons, we have performed high temperature MD simulation of protein unfolding. Histidine-containing phosphocarrier protein (HPr) was chosen because it is small (87 residues, Mr = 9315) and its crystal structure is known [11]. HPr consists of three a-helices (named A ~ C) and a four-stranded b-sheet (named b1 ~ b4) (Figure 1) [11].
Several MD simulations of temperature-induced protein unfolding have been reported. Fan et al. [12] performed high temperature (500 and 1000 K) vacuum MD simulation to study the molten globule state of a-lactalbumin. They found that constraining the helices does not stabilize the hydrophobic core, whereas constraining the hydrophobic core does stabilize the a-helices. Daggett & Levitt [13, 14] conducted a high temperature MD simulation of the unfolding of bovine pancreatic trypsin inhibitor (BPTI). They performed five simulations: native BPTI at 298 K and 423K and fully reduced BPTI at 298 K, 423 K, and 498 K. The reduced BPTI at high temperature indicated expansion of the protein. The authors concluded that the BPTI expansion was not caused by solvent penetration but by disruption of the packing interactions. Mark and van Gunsteren [15] performed MD simulations of the thermal denaturation of hen egg white lysozyme (500 K). They concluded that the lysozyme is still highly compact during the unfolding process, although the secondary structure was disrupted. MD simulations of apomyoglobin in water were performed by Brooks [16] at 312 K and by Tirado-Rives and Jorgensen [17] at 298K and at 358 K. In both simulations helices A, E, G and H were stable, while the other helices showed different behavior. This difference was due to the use of different destabilizing conditions. Caflisch and Karplus [18, 19] investigated the unfolding of barnase by high temperature MD simulations in the presence of explicit water molecules at 360 K and low pH, and at 600 K and neutral pH. They concluded that an essential step in the denaturation process is the separation of the major a-helix from the b-sheet, coupled to the exposure of the principal hydrophobic core, and that many non-polar side chains form hydrogen-bonds to water molecules. Li and Daggett [20] conducted MD simulations of the thermal unfolding of chymotrypsin inhibitor 2 (CI2) at 498K. They identified and characterized the major transition state of the unfolding process. They reported that in the transition state the molecule has a considerably weakened hydrophobic core, but that its overall structure is closer to that in the native rather than the unfolded state.
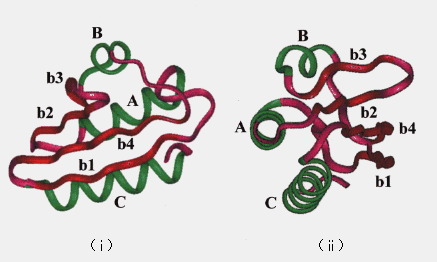
Figure 1. Backbone of the crystal structure of HPr. Helices (A ~ C) are drawn in black, strands (b1 ~ b4) are in gray, and loops are in white; (i) a view of one side, (ii) rotated 90 degrees with respect to the schematic diagram in (i).
In most of the previous MD simulations, the unfolding process was accelerated by extremely high temperature (400 to 1000 K). HPr is a very small (87 residues) and simple protein containing three a-helices and a b-sheet. Hence, we expected that HPr would undergo unfolding without any of the additional acceleration conditions used in other MD simulations such as unreasonably high temperature or low pH [12 ~ 20]. To elucidate details of the unfolding pathway, we performed MD simulation of HPr for 1 ns at 373K.
II. MATERIALS AND METHODS
1. Software for molecular dynamics
AMBER 3.0 Revision A [21] and a locally modified MD-module for the calculation of long-range electrostatic forces by twin-range methods (MD-MODIFIED) [22] were used throughout this study. The LINK, EDIT, and PARM modules were employed for construction of molecular topologies, generation of coordinates, and assignment of force field parameters, respectively. The MIN and MD-MODIFIED modules were used for energy-minimization and molecular dynamics, respectively. All calculations were performed on a Cray C916 super computer.
2. Generation of initial structure
The X-ray crystal structure of Streptococcus faecalis HPr [11] was used as the initial structure. An AMBER all atom force field [23] was employed during the simulations. The HPr structure was placed in a box filled with TIP3P water [24]. The box size (52 A × 46 A × 45 A) was chosen so that the minimum distance of any protein atom from the wall of the box was 7.0 A. Water molecules whose oxygens were located within 3.0 A or whose hydrogens were located within 2.8 A from the protein atoms were deleted. See Table I for other details of the simulation.
3. Molecular dynamics simulation
Two MD trajectories were generated, one at 300 K (room temperature simulation) and the other at 373 K (high temperature simulation). The energy of the initial structure was minimized until the norm of the gradient fell within 0.2 kcal/mol. In MD, all the covalent bonds were constrained to their equilibrium values by the SHAKE algorithm [25], and a time step of 2 fs was used. A twin-range method was employed to calculate nonbonded interactions [22,26], where the first cut-off was 7A and the second was 18 A (see the legend to Table I). Periodic boundary condition was applied to avoid the surface effect. The velocities were generated for the energy-minimized structure according to the Boltzmann distribution at 0.1 K. One hundred steps of classical molecular dynamics with a time step of 0.1 fs and with velocity scaling every 10 steps were performed to prevent failure in SHAKE during the following heating period. Heating was done up to 300 K for 10 ps (room temperature simulation) or 373 K (high temperature simulation) for 25 ps. The temperature was kept constant at 300 K or 373 K according to Berendsen et al. [27] with a time constant of 0.2 ps. The simulations were continued at 300 K for a further 190 ps (total 200 ps) and at 373 K for a further 975 ps (total 1 ns). An NTP (constant number of particles, temperature, and pressure) ensemble at a pressure of 1 atm with a relaxation time of 0.5 ps was employed [27].
Table I. Summary of simulation
| Number of atoms | 1307 (Protein)
7980 (Water)
9287 (Total)
|
| Nonbonded cutoff radius (A) | 7a
18b
|
| Number of nonbonded pairsc | 8.2 × 105 a
1.1 × 107 b
|
| Dielectric | 1
|
| Box size (A) | X = 52
Y = 46
Z = 45
|
| CPU time usage | 315 hours for 1000 ps
simulation (Cray C916)
|
a For proximal pairs, van der Waals, H-bond and
electrostatic forces were calculated for every time
step.
b For long-range pairs, electrostatic forces were
calculated once in 10 steps (immediately after up-
date of the pairlists) and used in the following 9
steps.
c Approximate values at 300 ps.
4. Analyses
The simulated structures were visualized by a graphic soft ware, Chemistry Viewer, on a Titan 1500 mini-super computer (Kubota Computer Co.). Analyses were performed using originally developed programs (References 22, 28 and this study).
III. RESULTS AND DISCUSSION
1. Global structure
The root mean square deviation (RMSD) of the heavy atoms from the crystal structure as a function of time is given in Figure 2. The room temperature simulation was stable for 200 ps. In the high temperature simulation (373 K), two structural transitions were observed. Following the initial transition (150 ~ 230 ps), the RMSD stabilized at approximately 7 A between 230 to 400 ps (the first intermediate; FI). After 400 ps, the RMSD began to drift again (the second transition 400 ~ 840 ps). After 840 ps, the RMSD stabilized at approximately 12 A (the second intermediate; SI). The deviation from the crystal structure observed during MD simulations was mostly distributed in the loop region of the structure, consistent with the other simulations (Figure 3) [13, 18].
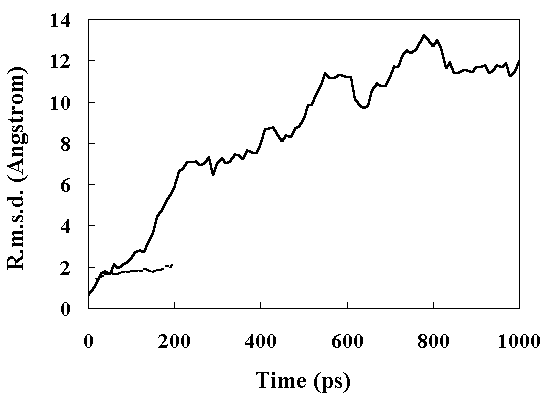
Figure 2. Main chain heavy atom RMS displacements of the simulated structures from the crystal structure. Continuous line, high temperature simulation; broken line, the room temperature simulation.

Figure 3. The RMS a-carbon displacements in the HPr from the X-ray structure as a function of residue number. Continuous line, the room temperature simulation (300 K, 150 ~ 200 ps); broken line, the high temperature simulation (373 K, 250 ~ 350 ps); dotted line, the high temperature simulation (900 ~ 1000 ps).
Figure 4 shows the residue RMS fluctuations (RMSF) calculated from the X-ray temperature factors [11] and from the simulated trajectories. The room temperature simulation reproduced the experimental results well, but both FI and SI obtained by the high temperature simulation showed larger fluctuations. In particular, the RMSF of the loop regions were larger than those of other parts of the structure (Figure 4), indicating increased mobility.
2. Solvent-accessible surface area
Solvent-accessible surface area (ASA) was calculated according to Shrake and Rupley [29]. The radius of the probe solvent was 1.4 A. Figure 5 shows the time course of the ASA during the simulations. At room temperature, the ASA was constant with an average value of 5187 A2 from 150 to 200ps (the ASA of the X-ray structure is 5162 A2). At high temperature the ASA increased gradually until about 600 ps, and then stabilized at a value of about 8500 A2 (Figure 5)(the ASA of the fully extended structure is 14224 A2). The ASA of the polar residues increased very slowly during the simulation (the ASA of the polar residues of the fully extended structure is 7813 A2), but exposure of the nonpolar residues to the solvent occurred until about 400 ps (Figure 5)(the ASA of the nonpolar residues of the fully extended structure is 6411 A2). The ASAs of the side-chains of polar residues are shown in Table II. Most of the hydrophobic residues were exposed to the solvent in the FI state. These results suggested that the first transition to FI caused the large RMSD and RMSF of the loop region of the structure (Figures 3 and 4), along with the exposure of the nonpolar residues to the solvent.
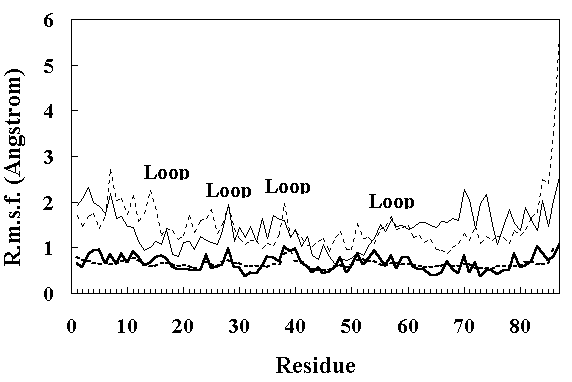
Figure 4. Main chain RMS fluctuations of the residues in HPr. The continuous thick line shows the RMS fluctuations calculated from the X-ray temperature factors [11]. The dotted thick line shows the RMS fluctuations calculated from the average values over the 150 ~ 200 ps period of the room temperature simulation. The thin continuous line and thin dotted line show the RMS fluctuations calculated from the average values over the 250 ~ 350 ps and 900 ~ 1000 ps period of the high temperature simulation, respectively.
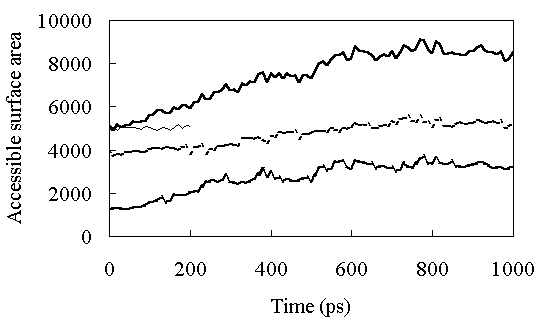
Figure 5. Solvent-accessible surface area (ASA) as a function of time. The continuous thick line shows ASA of the whole protein at high temperature. The continuous thin line shows ASA of the whole protein at room temperature. The dashed thick line shows ASA of hydrophobic residues in HPr, and the dotted thick line shows ASA of polar residues in HPr at high temperature.
3. Identification of the transition state
In the high temperature simulation, the first major structural change occurred around 150 ps (Figure 2). At 150 ps, A - C and b4 - C secondary structure element packings began to be disrupted (Figure 6). This resulted in opening of the hydrophobic core and exposure of the core residues to solvent. The unfolding of the hydrophobic core occurred very rapidly and most of the native hydrophobic contacts were lost during initial transition (150 ~ 230 ps)(Table II and Figure 5).
Based on observations, the structure at 150 ps appeared similar to that in the native state, except for helix C (Figure 7). Helix C was separated from the hydrophobic core in this state. However, no solvent molecules penetrated between A and C, and b4 and C secondary structure elements. Energetically, loss of van der Waals interactions within the protein due to the disruption of the hydrophobic core packing was not compensated by protein - solvent interaction. Therefore, the enthalpy of the system should be high. Correspondingly, the potential energy of the protein calculated from the coordinates at this state increased. At 150 ps, the protein was still relatively compact (Figures 5, 6 and 7), and the entropy was surmised to be a little higher than that in the native state. Thus, the free energy at this time point should be high, and consequently, the unfolding of the protein occurred quickly (Figure 2). From these considerations, we think the structure at 150 ps to be close to that in the transition state, which may be a transient intermediate. Li & Daggett reported similar characteristics in the transition state of CI2 unfolding [20].
Table II. Side chain ASA at 373 K
| Residues | X-ray structure | 250 ~ 350 psa | 900 ~ 1000 psa
|
| Phe 6 | 48.5 | 101.6 | 168.5
|
| Ile 8 | 0.0 | 117.9 | 141.4
|
| Ile14 | 0.0 | 111.5 | 121.0
|
| Val23 | 0.0 | 70.7 | 108.5
|
| Ala26 | 0.0 | 22.7 | 64.5
|
| Phe29 | 20.8 | 21.4 | 106.1
|
| Leu35 | 0.0 | 17.3 | 86.7
|
| Leu44 | 0.0 | 10.8 | 133.5
|
| Val55 | 0.0 | 105.0 | 64.9
|
| Val61 | 0.9 | 100.5 | 111.9
|
| Ile63 | 0.0 | 30.0 | 110.0
|
| Val65 | 0.0 | 32.6 | 103.4
|
| Ile77 | 0.0 | 45.6 | 120.2
|
| Leu86 | 0.0 | 108.7 | 218.6
|
| Ala87 | 53.4 | 176.6 | 120.5
|
| Totalb | 5162 | 6860 | 8514
|
a ASA time-averaged over a 100 ps period.
b The total ASA of HPr including polar
and nonpolar residues.
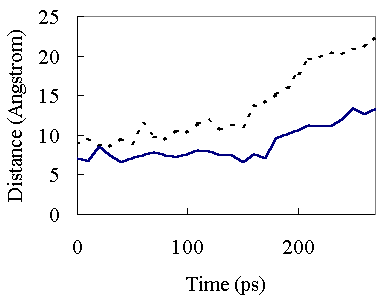
Figure 6. Interatomic Ca-Ca distances as a function of time at 373K. Continuous line, the distance between Ala26 Ca and Ile77 Ca atoms; broken line, the distance between Ile63 Ca and Ile77 Ca atoms. The 26 -77 and 63 - 77 distances refer to A - C and b4 - C hydrophobic packing, respectively.

Figure 7. Comparison of the simulated transition state structure with the crystal structure. Only the main chain is considered. See legend for Fig. 1 for colors of the secondary structures.
4. Secondary structure
Secondary structure was assigned based on the backbone dihedral angles, f and y. The residues are considered to reside in the helical region of the conformational space when f and yangles are within approximately 40o of the most commonly observed values in the helical regions of crystal structures (-100° <= f <= -30° ; -80° <= y <=-5°, where the canonical values are -63.8° ±6.6° and -41.0°
±7.2° for f and y, respectively [30]). The b-region was bounded as follows: -170° <= f <= -50°, 80° <= y <=190°. The secondary structure content of the simulated structure at high temperature was calculated with the requirement that at least three successive residues fulfill the angular criterion as described above at any one time.
The a-helices were stable during this simulation (percentage of a-helices within the HPr was about 40 %; Figure 8). In contrast to a-helices, the b-sheet content began to decrease at about 300 ps, and completely disappeared after 800 ps (Figure 8). These results indicated that FI retained most of its secondary structure, but SI retained only a-helices. In the case ofa-lactalbumin, most a-helix regions were stable while b-sheet regions were unfolded in the molten globule state, as revealed by NMR and CD spectroscopy [7, 31]. This suggests that SI of HPr is in a molten globule state.
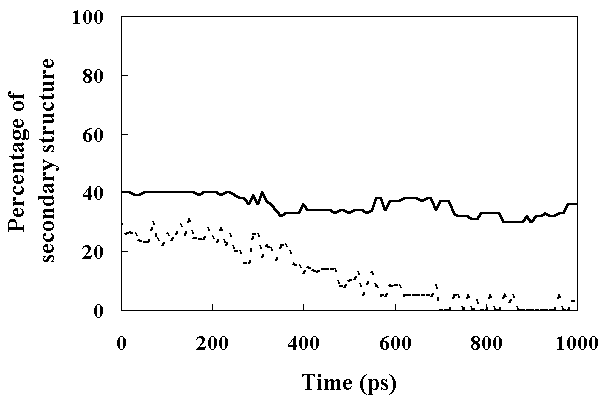
Figure 8. The percentage of the secondary structure present in HPr as a function of time. Secondary structure assignments were based on (f, y) angles with the added constraint that it should be a repeating structure with the participation of at least three successive residues (see text for details). The continuous line shows the percentage of a-helix and the dashed line shows the percentage of b-sheet.
5. Packing interactions
Figure 9 shows the residue-residue contacts present in the HPr crystal structure (upper-left diagonal of Figure 9 (A), (B) and (C)), in the averaged structure in the last 50 ps of the room
temperature simulation (lower-right diagonal of Figure 9 (A)), in the averaged structure from 250 to 350 ps in the high temperature simulation (FI state; lower-right diagonal of Figure 9 (B)), and in the averaged structure from 900 to 1000 ps in the high temperature simulation (SI state; lower-right diagonal of Figure 9 (C)).
(A)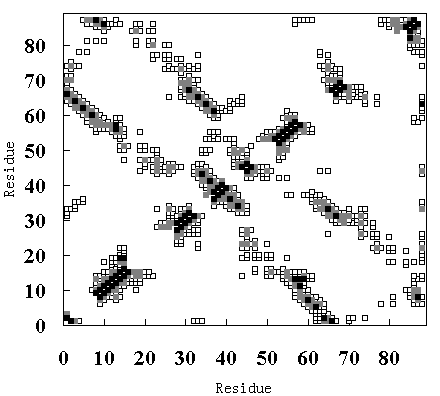
(B)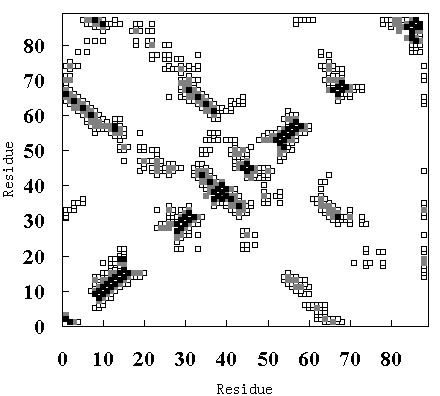
(C)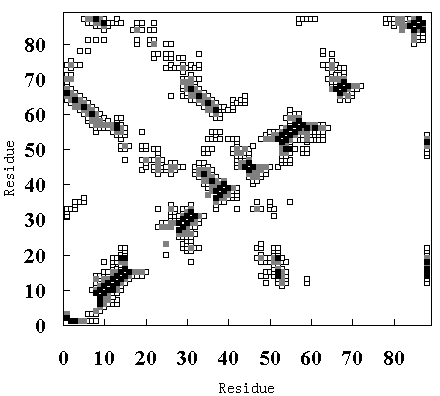
Figure 9. Tertiary contact maps. Crystal structure (upper-left diagonal of (A), (B) and (C)), room temperature simulation (lower-right diagonal of (A)), high temperature simulation during 250 to 350 ps (lower-right diagonal of (B)) and 900 to 1000 ps (lower-right diagonal of (C)). The darkest blocks represent Ca - Ca distances <= 5 A, the second lightest shade is for 5 A <= d <= 7 A, and the lightest shade is for 7 A <= d <= 10 A.
In the crystal structure, various tertiary contacts are evident (see detail for Table III), nearly all of which were maintained in the room temperature simulation (Figure 9 (A)). These tertiary contacts were also observed at the high temperature simulation between 250 and 350 ps (FI state; Figure 9 (B) and Table III). In contrast, most of the tertiary contacts were lost at high temperature between 900 and 1000 ps (SI state; Figure 9 (C) and Table III). In FI state several a-a, a-band b-bcontacts were observed, but in the SI state only an a-a contact (A - B) was observed (Table III), because the b-sheets had been disrupted. These results again indicate that SI exists in a molten globule state.
Table III. Percentage of tertiary contact

IV. CONCLUSION
We performed MD simulations of HPr to analyze the protein unfolding pathway. The simulation at room temperature was stable, but the protein underwent two-step unfolding at high temperature. Both the first and second intermediates fluctuated greatly. In particular, the loop regions deviated markedly from the crystal structure and showed large fluctuations, consistent with other high temperature simulations [13,18]. Most of the hydrophobic residues were exposed to the solvent during the first structural transition. All of the secondary structures were maintained in the first intermediate between the first and second transitions, but in the second intermediate, the b-sheet was completely lost although a-helices were stable. The tertiary contacts were fairly well maintained in the first intermediate; in contrast, those in the second intermediate were diminished.
The structure during the transition state of unfolding was identified from the high temperature MD simulation. The overall structure during the transition state was closer to that in the native than the unfolded state. The disruption of the hydrophobic packing of A - C and b4 - C, without solvent penetration was the first step of structural change from the native to transition state. The transition state occurred early in the unfolding process, and involved a transient intermediate (which quickly unfolded to another state).
To date no experimental data are available on the thermal unfolding of HPr. However, the unfolding of HPr based on our simulation was considered to involve the following ; (1) the disruption of hydrophobic packing, but no penetration to the inside of the opened secondary structure elements by water molecules (transition state), (2) increase of the mobility of the loop region and simultaneous exposure of the hydrophobic residues to the solvent (FI), and (3) cooperative disruption of the b-sheet and tertiary packing (SI) (Figure 10). We considered SI to be in a molten globule state because it showed large fluctuations and a considerable amount of the native secondary structure was preserved while the tertiary structure was completely destroyed.

Figure 10. Main chain trace of the averaged structures in the high temperature simulation of HPr. See legend to Fig. 1 for colors of the secondary structures.
V. ACKNOWLEDGEMENTS
We thank RIPS at the Agency of Industrial Science and Technology for providing time on the Cray C916 supercomputer. This work was partly supported by a research grant from the Sumitomo Foundation (to I. Y.) and by the RING Program of the Agency of the Industrial Science and Technology (to Y. K. and M. U.).
VI. REFERENCES
[1] Dolgikh, D.A., Gilmanshin, R. I., Brazhnikov, E. V., Bychkova, V. E., Semisotnov, G. V., Venyaminov, S. Y. and Ptitsyn, O. B. a-Lactalbumin: compact state with fluctuating tertiary structure? FEBS Letters 136: 311-315, 1981.
[2] Ptitsyn, O. B., Pain, R. H., Semisotnov, G. V., Zerovnik, E. and Razgulyaev, O. I. Evidence for a molten globule state as a general intermediate in protein folding. FEBS Letters 262: 20-24, 1990.
[3] Kuwajima, K. The molten globule state as a clue for understanding the folding and cooperativity of globular protein structure. Proteins 6: 87-103, 1989.
[4] Ohgushi, M. and Wada, A. 'Molten globule state' : a compact form of globular proteins with mobile side-chains. FEBS Letters 614: 21-24, 1983.
[5] Ptitsyn, O. B. The molten globule state. In: "Protein folding." (Creighton, T. E. eds.) p.243-p.300 (1992) W. H. Freeman, New York.
[6] Amir, D. and Haas, E. Reduced bovine pancreatic trypsin inhibitor has a compact structure. Biochemistry 27: 8889-8893, 1988.
[7] Baum, J., Dobson, C. M., Evans P. A. and Hanley, C. Characterization of a partly folded protein by NMR methods: studies on the molten globule state of guinea pig a-lactalbumin. Biochemistry 28: 7-13, 1989.
[8] Dobson, C. M. Unfolded proteins, compact states and molten globules. Curr. Opin. Struct. Biol. 201: 161-200, 1992.
[9] Harding, M. M., Williams, D. H. and Woolfson, D. N. Characterization of a partially denatured state of a protein by two-dimensional NMR: reduction of the hydrophobic interactions in ubiquitin. Biochemistry 31: 3120-3128, 1991.
[10] Hughson, F., Wright, P. and Baldwin, R. L. Structural characterization of a partly folded apomyoglobin intermediate. Science 249: 1544-1548, 1990.
[11] Jia, Z., Vandonselaar, M., Hengstenberg, W., Quail, J. W. and Delbaere L. T. J. The 1.6 A structure of histidine-containing phosphotransfer protein HPr from Streptococcus faecalis. J. Mol. Biol. 236: 1341-1355, 1994.
[12] Fan, P., Kominos, D., Kitchen, D. B., Levy, R. M. and Baum, J. Stabilization of a-helical secondary structure during high-temperature molecular-dynamics simulations of a-lactalbumin. Chemical Physics 158: 295-301, 1991.
[13] Daggett, V. and Levitt, M. A model of the molten globule state from molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 89: 5142-5146, 1992.
[14] Daggett, V. and Levitt, M. Protein unfolding pathways explored through molecular dynamics simulations. J. Mol. Biol. 232: 600-619, 1993.
[15] Mark, A. E. and van Gunsteren, W. F. Simulation of the thermal denaturation of hen egg white lysozyme: trapping the molten globule state. Biochemistry 31: 7745-7748, 1992.
[16] Brooks, C. L., III. Characterization of native apomyoglobin by molecular dynamics simulation. J. Mol. Biol. 227: 375-380, 1992.
[17] Tirado-Rives, J. and Jorgensen, W. L. Molecular dynamics simulations of the unfolding of apomyoglobin in water. Biochemistry 32: 4175-4184, 1993.
[18] Caflisch, A. and Karplus, M. Molecular dynamics simulation of protein denaturation: solvation of the hydrophobic cores and secondary structure of barnase. Proc. Natl. Acad. Sci. USA 91: 1746-1750, 1994.
[19] Caflisch, A. and Karplus, M. Acid and thermal denaturation of barnase investigated by molecular dynamics simulations. J. Mol. Biol. 252: 672-708, 1995.
[20] Li, A. and Daggett, V. Identification and characterization of the unfolding transition state of chymotrypsin inhibitor 2 by molecular dynamics simulations. J. Mol. Biol. 257: 412-429, 1996.
[21] Seibel, G., Singh, U. C., Weiner, P. K., Caldwell, J. and Kollman, P. A. AMBER 3.0 Revision A. University of California, San Francisco, CA. 1989.
[22] Komeiji, Y., Uebayasi, M., Someya, J. and Yamato, I. Molecular dynamics simulation of trp-aporepressor in a solvent. Prot. Engng. 4: 871-875, 1991.
[23] Weiner, S. J., Kollman, P. A., Nguyen, D. and Case, D. A. An all atom force field for simulations of proteins and nucleic acids. J. Compt. Chem. 7: 230-252, 1986.
[24] Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W. and Klein, M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79: 926-935, 1983.
[25] Ryckaert, J., Ciccotti, G. and Berendsen, H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23: 327-341, 1977.
[26] De Vlieg, J., Berendsen, H. J. C. and van Gunsteren, W. F. An NMR-based molecular dynamics simulation of the interaction of the lac repressor headpiece and its operator in aqueous solution. Proteins 6: 104-127, 1989.
[27] Berendsen, H. J. C., Postma, J. P. M., van Gunsteren, W. F., DiNola, A. and Haak, J. R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81: 3684-3690, 1984.
[28] Komeiji Y., Uebayasi M. and Yamato I. Molecular dynamics simulations of the trp apo- and holo-repressors: domain structure and ligand-protein interaction. Proteins 20: 248-258, 1994.
[29] Shrake, A. and Rupley, J. A. Environment and exposure of solvent of protein atoms. Lysozyme and Insulin. J. Mol. Biol. 79: 351-371, 1973.
[30] Presta, L. G. and Rose, G. D. Helix signals in proteins. Science 240: 1632-2682, 1988.
[31] Chyan, C.-L., Wormald, C., Dobson, C. M., Evans, P. A. and Baum, J. Structure and stability of the molten globule state of guinea-pig alpha-lactalbumin: a hydrogen exchange study. Biochemistry 32: 5681-5691, 1993.
 Return
Return

 Return
Return










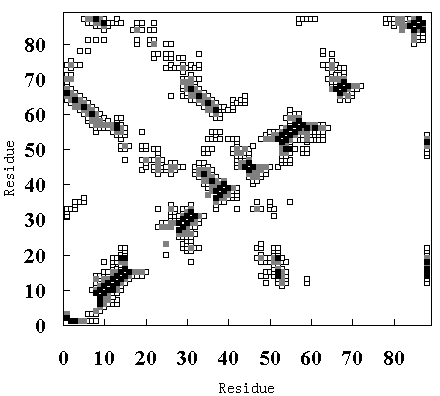


 Return
Return