Evaluation of Enthalpies of Benzene-Monosubstituted Benzene interactions by Semi-Empirical MO Calculations. Their Relationship to the Experimental Enthalpies Determined by GLPC
Tadashi ENDO, Takahiro IIDA, Nobuhide FURUYA, Yumiko YAMADA and Masato M. ITO
 Return
Return
1 Introduction
Precise molecular recognition is essential to living systems. For example, the following biological discrimination is well known: enzyme-substrate [1], antigen-antibody [2], nucleic acid-protein [3], drug-receptor [4], and hormone-receptor recognition [5]. In contrast, a very large number of studies have recently been made on chemical recognition mainly using various model compounds of host-guest type such as crown ethers [6], criptands [7], calixarenes [8], and convergent cleft molecules [9]. It is now accepted that molecular recognition, whether biological or chemical [10], is due to specific weak (noncovalent) interactions between interacting groups in the respective molecules.
Concerning weak interactions between groups, comparable in energies (or enthalpies) to van der Waals interactions, experimental studies have extensively been made. These include dipole-induced dipole interaction between the 1,3-dioxane and phenyl rings [11], an alkyl-phenyl interaction [12], an alkyl-alkyl interaction [13] including that between two t-butyl groups [14], and so on. In addition, recent theoretical studies on aromatic-aromatic interactions suggested an energetically favorable orientation of two aromatic rings as well as their interaction energies [15 - 17].
We have been studying factors controlling such precise molecular recognition as occurs in living systems, by use of a pair of acylurea derivatives [open chain analogues of pyrimidine bases (e.g., uracil and thymine)] which can associate strongly with each other as well as with themselves [18]. As a result, it has been clarified that (i) intermolecular association is the first requirement for molecular recognition [19], (ii) three-dimensional shape similarity between interacting groups in reacting molecules is responsible for more specific and precise molecular recognition than would otherwise be achieved [20].
These findings led us to investigate weak interactions between interacting groups. Using GLPC, it has been demonstrated that (i) enthalpies of weak interactions of a phenyl group (DDHt)with substituted benzenes [21], alkanes [22], alkenes [23], ethers [23], and carbonyl compounds [21] range from -2.7 to +0.1 kcal mol-1 (1 cal = 4.184 J) and (ii) methylation or methoxylation of a benzene ring weakens or strengthens, respectively, the phenyl-phenyl interaction [21]. Further examinations have revealed that degree of the recognition between molecules each having a nonpolar group can be controlled by the strength of shape-specific weak interactions between nonpolar groups in the respective molecules [24].
The above-mentioned experimental enthalpies of the interactions [21] can only be determined with a phenyl group as one component, because of limitation of stationary liquids available in GLPC. Thus, some theoretical approaches to evaluate weak interactions between relatively nonpolar molecules will help to elucidate an entire picture of the weak interactions including their shape-specificity. This approach need not be very accurate and quantitative; it should, however, be (i) precise enough to bring about good correlation with experimental results and (ii) convenient enough to make it possible to calculate the interaction energies between the phenyl and a wide variety of groups within a realistic time.
Ab initio calculations seem not to be suitable for this purpose; they require enormous time and resources of the computer because of complicated calculations of configuration interactions (CI) using a large number of basis sets, the calculation methods being still a subject of theoretical chemists even for the intermolecular interaction of a methane dimer [25]. There appear to have been no calculation methods available for electron correlation which enable calculations of interactions between benzene and substituted benzenes to be precise enough within a realistic time. On the other hand, for semi-empirical methods such as PM3 in MOPAC where (i) CI calculations are not implemented explicitly and (ii) the effect corresponding to electron correlation is supposed to be incorporated implicitly in the set of adjustable parameters, the use of which is characteristic of semi-empirical calculations. This is evident from the fact that heats of formation for various organic compounds can be evaluated with considerable accuracy by means of MOPAC [26].
With this situation in mind, MOPAC was used to evaluate enthalpies of intermolecular interactions, and the effectiveness and limitations of the semi-empirical method were examined. In this paper, we wish to report that the calculated enthalpies of weak interactions between benzene and various substituted benzenes have close correlation with the corresponding experimental enthalpies determined by GLPC.
2 Calculation methods
All calculations were carried out with the MOPAC93 program [27] for Power Macintosh (CS MOPAC, Fujitsu Ltd.) on Apple Power Macintosh 7200/120.
As monosubstituted benzenes (PhX), anisole (PhOMe), benzene (PhH), chlorobenzene (PhCl), N,N-dimethylaniline (PhNMe2) , ethylbenzene (PhEt), fluorobenzene (PhF), nitrobenzene (PhNO2) , and toluene (PhMe) were used.
As initial arrangements of a pair of benzene and a monosubstituted benzene (PhH-PhX system), one parallel (P) and four vertical arrangements (Vr , Vp , Vm , and Vb) were chosen (Figure 1a). In P arrangement, two benzene rings of PhH and PhX molecules are stacked parallel to each other. In Vr arrangement, the lowest H atom of PhH points to the center of the benzene ring of PhX. In Vp (Figure 1b) or Vm arrangement, the lowest H atom at the para or meta position, respectively, to substituent X is located above the centroid of PhH. In Vb arrangement, substituent X lying at the lowest position ("bottom") of PhX is located above the centroid of PhH.
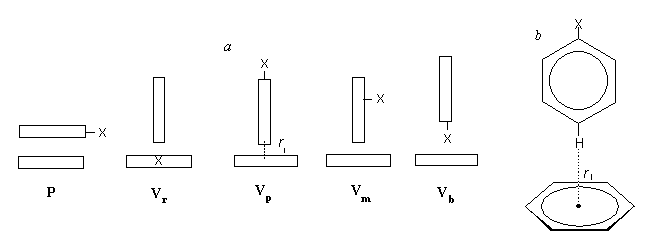
Figure 1. (a) Schematic drawings of initial arrangements (P, Vr , Vp , Vm , and Vb) of benzene (PhH)-monosubstituted benzene (PhX) systems; (b) a drawing of initial arrangement Vp. The symbol rI represents an initial intermolecular distance; for definition, see the text. The symbol X shows a substituent of benzene. In the case of Vb arrangement, the rI for X = Me, Et, MeO, NMe2, or NO2 is the distance between the H atom in these groups (except for a NO2 group [the O atom instead of the H atom]) and the "closest" C atom in PhH; for X = NMe2 or NO2, the N atom in these two groups is located above the centroid of PhH. In view of van der Waals radii of Cl (1.80 A), F (1.35 A), and O (1.40A), the rI values set up for these are 3.50, 3.05, and 3.1 A, respectively. For the other type of initial arrangement Vr (VrR) where a PhH molecule located above a PhX molecule is rotated by 90° relative to PhX, the DDHf values are also evaluated.
In the case of V arrangements, an intermolecular distance is defined as the distance between the centroid of a benzene ring lying on a plane and the lowest atom (H or X) of the other PhH or PhX molecule located above the centroid of the former benzene ring (Figure 1). With P arrangement, an intermolecular distance is defined as the distance between the facing "above" and "below" carbon atoms of two benzene rings of parallel orientation.
Setting up of an initial intermolecular distance (rI) was performed using Chem3D (CambridgeSoft Corp.) ver. 3.5 by geometrical calculation so that the rI may become the desired value (e.g., 2.60, 2.75, 3.05, 3.20, or 3.40 A). In the case of Vb arrangement, setting up of the rI is shown in the caption of Figure 1.
Energy minimization (geometry optimization) was carried out in the following way both for a single molecule (PhH or PhX) and for a pair of molecules (PhH-PhX system), thereby giving their heats of formation (DHf) : (1) in the case of a single molecule, the structure preliminarily optimized by Chem3D was subject to geometry optimization with MOPAC calculation; (2) with a PhH-PhX system, (i) its initial arrangement (Figure 1) was set up, using the optimized structures of a PhH molecule and a single PhX one mentioned above, (ii) the rI was then set up, and (iii) energy minimization was performed with MOPAC calculation.
In general, enthalpy of interaction (DDHf) between A and B molecules can be defined as Eq. 1, where DHf (A-B) is heat of formation of coexisting A and B molecules, DHf (A) is that of A
DDHf = DHf (A - B) - {DHf (A) + DHf (B)} (1)
molecule, and DHf (B) is that of B molecule.
3 Results and discussion
PhH-PhH Interactions
Evaluation of interaction enthalpies (DDHf) of benzene-benzene interaction for initial arrangement V was performed with three methods (MNDO, AM1, and PM3) and the results were compared with one another (Table 1). In view of the fact that (i) a half of thickness of a benzene ring is 1.7 A and (ii) van der Waals radius of an H atom is 1.2 A, heats of formation (DHf) were calculated, with structures optimized for various initial intermolecular distances (rI) of 2.60, 2.75, 3.05, and 3.20 A. The intermolecular distance ( ro ) optimized with PM3 method, for instance, was ca. 2.5 A, irrespective of the rI. The corresponding DHfs for initial structure V were 46.53 (rI = 3.20 A), 46.48 (3.05 A), 46.35 (2.75 A), and 46.29 kcal mol-1 (2.60 A), whereas those for the optimized structures were all 46.26 kcal mol-1, regardless of the rI. It has been clarified that (i) MNDO and AM1 methods tend to overestimate the intermolecular interactions and (ii) PM3 method is most suitable since it gives the DDHf values close to the experimental interaction enthalpy (DDHt) of -1.32 kcal mol-1 (X = H) [28].
Table 1 Effect of calculation methods on the DDHf for initial arrangements V and P of PhH-PhH systema
| rI /A | DDHf / kcal mol-1
|
|---|
MNDO
(V) | AM1
(V) | PM3
(P) | PM3
(V)
|
|---|
| 2.60 | -4.29 | -2.96 | 0.06 | -0.52
|
| 2.75 | -4.30 | -2.94 | 0.06 | -0.52
|
| 3.05 | -4.29 | -2.95 | 0.06 | -0.52
|
| 3.20 | -4.29 | -2.96 | 0.06 | -0.52
|
a The following key words were chosen for PM3 method. (1) For a PhH or PhX molecule: PM3 EF XYZ PRECISE GNORM = 0.01; (2) for a PhH-PhX system: PM3 EF XYZ PRECISE GNORM = 0.05 LET DDMIN = 0.0.
It is also evident from the data in Table 1 that the DDHf values by PM3 method for V and P arrangements (X = H) are -0.52 and 0.06 kcal mol-1, respectively, regardless of the rI. Since the experimental interaction enthalpy (DDHt) for X = H is -1.32 kcal mol-1, V arrangement appears to be more suitable as an initial arrangement of the system than P arrangement.
An optimized intermolecular distance for the benzene dimer was shown to be 5.0 A between their centroids (dcb-cb) by ab initio calculations [16, 29], molecular dynamics simulations [30], and Monte Carlo simulations [31]. In the present work, the dcb-cb becomes 4.978 A [32], the distance practically equal to that obtained by the previous work mentioned above.
Ab initio calculations of the benzene dimer indicated that interplanar angles (dihedral angles) between interacting benzene molecules approaching 90°, the "T-stacked" arrangement, are enthalpically favorable [16]. Moreover, when they adopt edge-to-face stacked orientation [17], electrostatic interaction between two benzene rings is reported to be attractive (-1.4 kcal mol-1). These findings agree with our result that the optimized geometry, which leads to close relationship between the DDHf and DDHt , is similar to the initial arrangement of vertical type (V). The T-shaped orientation of two benzene molecules is well recognized in four kinds of studies: (i) crystal structures of benzene [33], peptides (and proteins) [15], and organic compounds [34], (ii) molecular beam electric deflection studies [35], (iii) NMR studies [36], and (iv) theoretical calculations [30, 31, 37].
As to interaction energy, ab initio calculations of the benzene dimer for various orientations [16] revealed that the interaction energy minimum was ca. -2.4 kcal mol-1; a similar result was obtained by more recent calculations that the interaction energy for the T-shaped structure was -2.64 kcal mol-1 [29, 38, 39]. Moreover, NMR studies showed the enthalpy (DH ) of the benzene-benzene interaction to be ca. -2.0 kcal mol-1 [40], the DH value corresponding to theDDHt of -1.32 kcal mol-1 for X = H; transfer of a benzene molecule from an environment of saturated hydrocarbon molecules into an environment of benzene molecules is energetically favorable to an extent ranging to ca. -l kcal mol-1 [41]. These theoretical and experimental results suggest the enthalpy of PhH-PhH interaction to be ca. -l to -2 kcal mol-1. Accordingly, the calculated enthalpy (DDHf) of the PhH-PhH interaction by PM3 method might be more positive by ca. 0.5 kcal mol-1 or more.
PhH-PhX Interactions
As mentioned above, the calculated enthalpy (DDHf) of the PhH-PhH interaction was satisfactory in comparison with interaction energies (or enthalpy) obtained with ab initio calculations and with the experiment. Thus, the DDHf values were further calculated for various PhH-PhX systems in the case of the five initial arrangements. As the rI, 2.75 A was chosen, because the optimized intermolecular distance ( ro ) for X = H has been shown to be all 2.5 A except for P arrangement ro =5.41A), regardless of the rI [42], and because the sum -- (a half of thickness of a benzene ring) + (van der Waals radius of a H atom) -- is 2.9 A.
Figure 2 depicts a plot of the DDHf against the DDHt for initial arrangement P ( rI = 2.75 A). Arrangements after geometry optimization (optimized geometries) have been found to resemble the initial arrangement P. For most pairs, the PhH-PhX interactions are slightly repulsive. Optimized intermolecular distances ( ro ) change from 4.7 to 5.5 A. There exists no appreciable relationship between the DDHf and DDHt.
In the case of initial arrangement Vr ( rI = 2.75 A), the PhH-PhX interactions are all attractive, ranging in enthalpies markedly from -0.5 to -5.5 kcal mol-1. Optimized geometries resemble initial arrangement Vr except for (i) an unreasonable vertical arrangement[VP arrangement](X = Me) where two H atoms facing each other (an H atom of the methyl group in PhMe and an H atom in PhH) are penetrated to each other within the van der Waals radius; (ii) an unreasonable arrangement where the two benzene rings are aligned on the same plane ("coplane") in an edge-to-edge manner, with the two closest H atoms in the respective ring being penetrated to each other within the van der Waals radius[CP arrangement](X = Et); (iii) twisted CP -- another CP-like abnormal arrangement where the two benzene rings are twisted perpendicularly to each other[CP* arrangement](X = F). Furthermore, the ro values alter from 1.7 to 2.5 A. There is no appreciable relationship between theDDHf and DDHt , even if the points for the above-mentioned unreasonable arrangements are excluded.
For initial arrangement Vb , the PhH-PhX interactions are repulsive for X = Me, F, and NO2 , while attractive for the other Xs. Optimized geometries are similar to initial arrangement Vb except for (i) X = Et ( CP* arrangement) and (ii) X = OMe and NMe2 (arrangements somewhat different from Vb arrangement). Moreover, the ro values alter greatly from 1.7 to 5.6 A. The DDHf bears no appreciable relationship to the DDHt .
The DDHf values for initial arrangement Vp (rI = 2.75 A) are listed in Table 2, together with the DDHt values for reference. It has been clarified that (i) optimized geometries are similar to initial arrangement Vp regardless of both the rI and X and (ii) weak interactions between PhH and PhX are all attractive; the ro values for each system remain almost unaltered with the rI (ca. 2.4 to 2.5 A). A close relationship has been found to exist between the DDHf and DDHt (Figure 3), the correlation coefficient (r) being as large as 0.94.
Table 2 Initial arrangements Va, optimized intermolecular distances ( ro ), The DDHf (rI = 2.75 A), and the DDHt [21]
| PhX | Vp | Vm
|
|---|
| ro /A | DDHf | ro /A | DDHf | DDHt
|
|---|
| kcal mol-1 | kcal mol-1 | kcal mol-1
|
|---|
| PhEt | 2.51 | -0.49 | 2.51 | -0.50 | -1.09
|
| PhMe | 2.51 | -0.50 | 2.51 | -0.50 | -1.18
|
| PhF | 2.48 | -0.64 | 2.48 | -0.67 | -1.26
|
| PhCl | 2.49 | -0.61 | 2.48 | -0.63 | -1.29
|
| PhH | 2.50 | -0.52 | 2.50 | -0.52 | -1.32
|
| PhOMe | 2.45 | -0.80 | 2.50 | -0.53 | -1.51
|
| PhNMe2 | 2.43 | -0.80 | 2.51 | -0.48 | -1.58
|
| PhNO2 | 2.45 | -0.91 | 2.54 | -1.24 | -1.84
|
a In the case of Vp arrangement, differences in the ro between the rI values of 2.75 and 3.05 A are all within 0.01 A, and differences in the DDHf between the rI values of 2.75 and 3.05 A are all within 0.01 kcal mol-1.
In the case of initial arrangement Vm (rI = 2.75A), PhH-PhX interactions are also all attractive (Table 2). Optimized geometries are all similar to initial arrangement Vm . Further, the ro values remain almost unaltered with the systems (ca. 2.5A). However, the DDHf appears to have no appreciable relationship to the DDHt (Figure 4).
The DDHf for the electron-donating group (OMe or NMe2) is more negative with Vp than with Vm , whereas the DDHf for the NO2 group is more negative with Vm than with Vp (Table 2). Further, the Vp and Vm arrangements are interconvertible simply by rotating the upper benzene ring in PhX (Figure 1b) around its C6 axis by 60 degrees. Thus each system would be able to adopt either Vp or Vm arrangement, for which the DDHf value is more negative. On this basis, of the DDHf values for the two arrangements, the more negative value was selected for each system and plotted against the DDHt values (Figure 5). A close relationship has also proved to exist between the DDHf and DDHt , with the r being 0.94. In addition, the differences between the experimental DDHt values and the "DDHt" values calculated from the equation shown in Figure 5 have turned out to be ca. 0.1 kcal mol-1 or smaller.
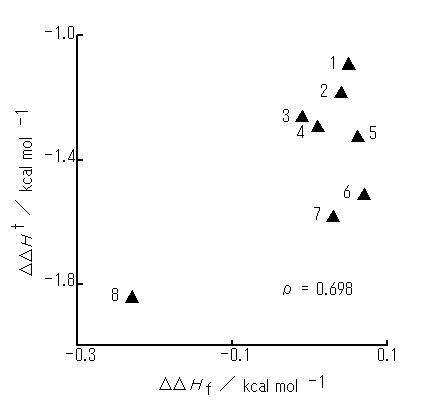
Figure 2. A plot of the DDHf optimized from initial arrangement P (rI = 2.75 A) against the DDHt. The numbers show substituents X of PhX: 1, ethyl; 2, methyl; 3, fluoro; 4, chloro; 5, H; 6, methoxy; 7, dimethylamino; 8, nitro group. All optimized geometries are similar to P arrangement ( ). In the case of rI = 3.40 A, (1) the DDHf values are equal to those for rI = 2.75 A except for (i) X = NMe2 (more positive by 0.07 kcal mol-1) and (ii) X = Et (more negative by 2.07 kcal mol-1) and (2) optimized geometries are similar to P arrangement except for X = Et (an arrangement similar to Vr).
). In the case of rI = 3.40 A, (1) the DDHf values are equal to those for rI = 2.75 A except for (i) X = NMe2 (more positive by 0.07 kcal mol-1) and (ii) X = Et (more negative by 2.07 kcal mol-1) and (2) optimized geometries are similar to P arrangement except for X = Et (an arrangement similar to Vr).
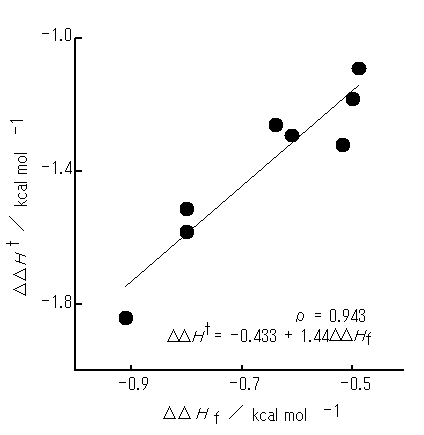
Figure 3. A plot of the DDHf optimized from initial arrangement Vp (rI = 2.75 A) against the DDHt. PhX molecules used are as in Figure 2. Optimized geometries are similar to Vp arrangement ( ) except for X = MeOand NMe2 (arrangements somewhat different from Vp ).
) except for X = MeOand NMe2 (arrangements somewhat different from Vp ).
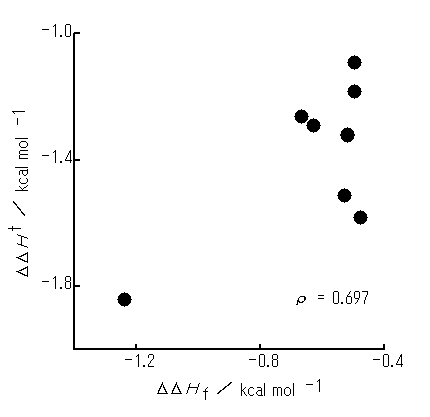
Figure 4. A plot of the DDHf optimized from initial arrangement Vm (rI = 2.75 A) against the DDHt. PhX molecules used are as in Figure 2. All optimized geometries are similar to Vm arrangement.
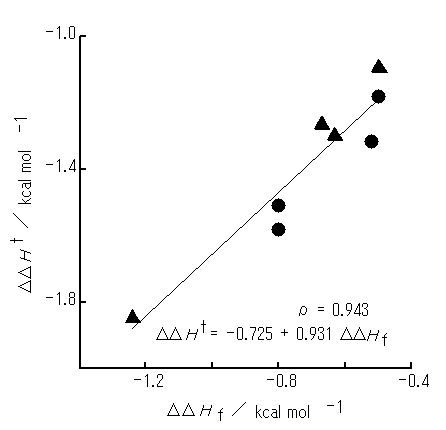
Figure 5. A plot of the DDHf optimized from initial arrangement Vm or Vp (rI = 2.75 A) against the DDHt. PhX molecules used are as in Figure 2. The DDHf values are taken from that for either Vm or Vp arrangement:  , from Vp;
, from Vp;  , from Vm.
, from Vm.
The results described here demonstrate that it is the initial arrangement Vp or Vm that brings about close relationship between the theoretical interaction enthalpies (DDHf) and the experimental ones (DDHt).
4 Conclusion
The present work has clarified that enthalpies of weak interactions between benzene (PhH) and monosubstituted benzenes (PhX) can be evaluated by MOPAC93 semi-empirical MO method, the calculated enthalpies having close relationship to the experimental ones, when (i) PM3 method is used as a calculation method and (ii) the initial arrangement of the PhH-PhX system is of the vertical type, in which the lowest H atom at the para or meta position to X in PhX is located above the centroid of PhH. Further, for X = H , the optimized intermolecular distance and optimized geometry [43] are consistent with those obtained with the ab initio calculations.
Evaluation of intermolecular interactions by means of ab initio MO method requires incorporation of electron correlation, for which calculations of considerably large configuration interactions (CI) are necessary. On the other hand, in the case of MOPAC methods such as PM3, it would not be unreasonable to consider that the DDHf (a measure of weak intermolecular interactions), essentially the difference between the DHs (heats of formation), is expected to be evaluated nearly as precisely as the DH themselves.
This is the first example in which theoretical enthalpies of the weak interactions between various pairs of aromatic molecules bear close correlation with the experimental enthalpies. The results presented here encourage us to evaluate enthalpies of weak interactions between benzene and a variety of molecules such as other substituted benzenes and alkenes by semi-empirical MO methods.
We thank Mr. Mitsuru Koike for valuable assistance.
References
[ 1] Holler, E., Angew. Chem. Int. Ed. Engl., 17, 648 (1978).
Dixon, M., Webb, E. C., Thorne, C. J. R. and Tipton, K. F., Enzymes, (3rd. ed.), Longman, London (1979), chap. VI.
Cramer, F. and Freist, W., Acc. Chem. Res., 20, 79 (1987).
[ 2] Capra, J. D. and Edmundson, A. B., Sci. American, 236, Jan. 50 (1977).
[ 3] Smith, H. O., Science, 205, 455 (1979).
McKnight, S. L., Sci. American, Apr. 32 (1991).
[ 4] Ariens, E. J., Drug Design (Vol. I), Ed. by Ariens, E. J., Academic Press, New York (1971), chap. 1.
[ 5] Lubke, K., Schillinger, E. and Topert, M., Angew. Chem. Int. Ed. Engl., 15, 741 (1976).
[ 6] Cram, D. J., Angew. Chem. Int. Ed. Engl., 27, 1009 (1988).
[ 7] Lehn, J.-M., Angew. Chem. Int. Ed. Engl., 27, 89 (1988).
[ 8] Bohmer, V., Angew. Chem. Int. Ed. Engl., 34, 713 (1995).
[ 9] Rebek, J., Jr., Angew. Chem. Int. Ed. Engl., 29, 245 (1990).
[ 10] Schneider, H.-J., Angew. Chem. Int. Ed. Engl., 30, 1417 (1991).
[ 11] Stoddart, J. F., Chem. Soc. Rev., 8, 85 (1979) and references cited therein.
[ 12] Watson, A. E. P., McLure, I. A., Bennett, J. E. and Benson, G. C., J. Phys. Chem., 69, 2753 (1965).
Zushi, S., Kodama, Y., Fukuda, Y., Nishihata, K. , Nishio, M., Hirota, M. and Uzawa, J., Bull. Chem. Soc. Jpn., 54, 2113 (1981).
Hiraki, Y. and Tai, Chem. Lett., 1982, 341.
[ 13] Berg, U., Liljefors, T., Roussel, C. and Sandstrom, J., Acc. Chem. Res., 18, 80 (1985).
[ 14] Lyttle, M. H., Streitwieser, A., Jr. and Kluttz, R. Q., J. Am. Chem. Soc., 103, 3232 (1981).
Carter, R. E. and Stilbs, P., J. Am. Chem. Soc., 98, 7515 (1976).
[ 15] Burley, S. K. and Petsko, G. A., Science, 229, 23 (1985).
[ 16] Burley, S. K. and Petsko, G. A., J. Am. Chem. Soc., 108, 7995 (1986).
[ 17] Hunter, C. A., Chem. Soc. Rev., 1994, 101 and references cited therein.
[ 18] Endo, T., Top. Curr. Chem., 128, 91 (1985).
[ 19] Endo, T., Kuwahara, A., Tasai, H., Murata, T., Hashimoto, M. and Ishigami, T., Nature, 268, 74 (1977).
[ 20] Endo, T., Tasai, H., Miyazawa, K., Endo, M., Kato, K., Uchida, A., Ohashi, Y. and Sasada, Y., J. Chem. Soc., Chem. Commun., 1983, 636.
[ 21] Ito, M. M., Kato, J., Takagi, S., Nakashiro, E., Sato, T., Yamada, Y., Saito, H., Namiki, T., Takamura, I., Wakatsuki, K., Suzuki, T. and Endo, T., J. Am. Chem. Soc., 110, 5147 (1988).
[ 22] Endo, T., Ito, M. M., Yamada, Y., Saito, H., Miyazawa, K. and Nishio, M., J. Chem. Soc., Chem. Commun., 1983, 1430.
[ 23] Endo, T., Ito, M. M. and Namiki, T., J. Chem. Soc., Chem. Commun., 1985, 933.
[ 24] Endo, T., Tajima, K., Yamashita, M., Ito, M. M., Nishida, J. and Ogikubo, T., J. Chem. Soc., Chem. Commun., 1986, 1561.
[ 25] Tsuzuki, S., Uchimaru, T. and Tanabe, K., Chem. Phys. Lett., 287, 202 (1998).
[ 26] Kihara, H., Uchida, N. and Ikuta, S., Bunshi Kido Ho (Molecular Orbital Method), Ed. by Osawa, E, Kodansha, Tokyo (1994), p62.
[ 27] Stewart, J. J. P., MOPAC93, Revision 2, Fujitsu Ltd., Nakase, Chiba, 261, Japan (1994).
[ 28] The DDHt is the enthalpy of the weak interaction of a PhX molecule with the phenyl group in the stationary liquid (practically PhH molecule) relative to the enthalpy of that of a n-octane molecule with the phenyl group.
[ 29] Hobza, P., Selzle, H. L. and Schlag, E. W., J. Phys. Chem., 97, 3937 (1993).
[ 30] Linse, P., J. Am. Chem. Soc., 115, 8793 (1993).
[ 31] Jorgensen, W. L. and Severance, D. L., J. Am. Chem. Soc., 112, 4768 (1990).
[ 32] dcb-cb = 2.50 ( ro ) + 1.086 (C-H bond length of PhH) + 1.392 (C-C bond length of PhX) = 4.978 A
[ 33] Cox, E. G., Cruickshank, D. W. J. and Smith, J. A. S., Proc. R. Soc. London A, A247, 1 (1958).
[ 34] Slawin, A. M. Z., Spencer, N., Stoddart, J. F. and Williams, D. J., J. Chem. Soc., Chem. Commun., 1987, 1070.
[ 35] Steed, J. M., Dixon, T. A. and Klemperer, W., J. Chem. Phys., 70, 4940 (1979).
[ 36] Laatikainen, R., Ratilainen, J., Sebastian, R. and Santa, H., J. Am. Chem. Soc., 117, 11006 (1995).
[ 37] Price, S. L. and Stone, A. J., J. Chem. Phys., 86, 2859 (1987).
Chipot, C., Jaffe, R., Maigret, B., Pearlman, D. A. and Kollman, P. A., J. Am. Chem. Soc., 118, 11217 (1996).
[ 38] An ab inito study [29] of interaction energies of the benzene dimer, however, showed that the parallel-displaced structure is slightly more stable than the above-mentioned T-shaped one by 0.88 kcal mol-1. Similarly, a favorable offset face-to-face p-stacked geometry is predicted using a simple model of the charge distribution in a p-system [Hunter, C. A. and Sanders, J. K. M., J. Am. Chem. Soc., 112, 5525 (1990)].
[ 39] It has been suggested that the interaction energy for the benzene dimer calculated with ab initio method depends significantly upon the basis set implemented and the method for electron correlation calculation applied [Hobza, P., Selzle, H. L. and Schlag, E. W., J. Phys. Chem., 100, 18790 (1996)].
[ 40] Slejko, F. L., Drago, R. S. and Brown, D. G., J. Am. Chem. Soc., 94, 9210 (1972).
[ 41] Jencks, W. P., Catalysis in Chemistry and Enzymology, McGraw-Hill, New York (1969), p415.
[ 42] Optimized intermolecular distances ( ro ) are somewhat shorter than the sum of a half of thickness of a benzene ring and van der Waals radius of an H atom. This might be because the H atom in PhX is located just above the centroid of the other benzene ring.
[ 43] The PM3 MOPAC calculations have revealed that PhH-PhX pairs sometimes adopt irrational structures (e.g., CP and CP*) in which a pair of closest H atoms in the interacting benzene rings are located within the van der Waals spheres. It should be noted that these unreasonable structures are occasionally more "stable", namely, have apparently more negative heats of formation than the realistic ones. Thus, when optimized geometries and/or energetics are studied using the MOPAC program for intra- or intermolecular systems composed of two (or more) aromatic rings, one had better examine whether a non-realistic structure having such an irrationally close contact of the rings is "stabilized" or not.
 Return
Return
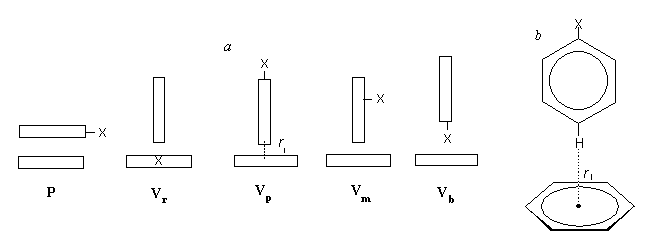
 Return
Return
 ). In the case of rI = 3.40 A, (1) the DDHf values are equal to those for rI = 2.75 A except for (i) X = NMe2 (more positive by 0.07 kcal mol-1) and (ii) X = Et (more negative by 2.07 kcal mol-1) and (2) optimized geometries are similar to P arrangement except for X = Et (an arrangement similar to Vr).
). In the case of rI = 3.40 A, (1) the DDHf values are equal to those for rI = 2.75 A except for (i) X = NMe2 (more positive by 0.07 kcal mol-1) and (ii) X = Et (more negative by 2.07 kcal mol-1) and (2) optimized geometries are similar to P arrangement except for X = Et (an arrangement similar to Vr).
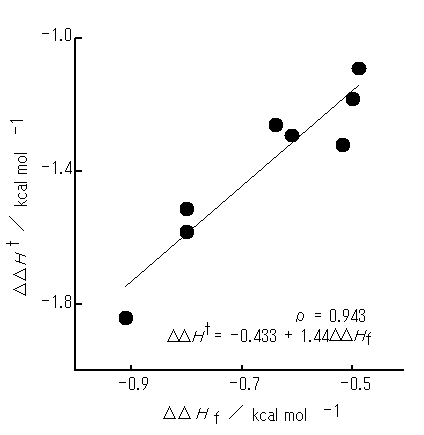
 ) except for X = MeOand NMe2 (arrangements somewhat different from Vp ).
) except for X = MeOand NMe2 (arrangements somewhat different from Vp ).

