Crystal Structure Model-Assembly Program Using the Monte Carlo and the R-factor Method
Hiroyuki MIURA and Takeshi KIKUCHI
 Return
Return
1 Introduction
The Rietveld method is an effective tool to determine the precise crystal structure of powder crystalline materials. It refines crystal structure parameters such as atomic coordinates and temperature factors. However, the Rietveld method can not find structure models by itself, since it requires a starting model. Relatively correct initial data must be prepared to solve the non-linear equation. In other words, the structure model of the target material must be provided. When no structural information about the material is available, it is very difficult to make a structure model. In a previous paper, we proposed a calculation program based on a packing analysis method [1]. This program searches suitable atom arrangements in a given unit cell from a simple rule stating that "inter-atomic distances must be larger than the sum of each atomic radius." This method was useful to find the atomic arrangements of simple inorganic materials. However, in the case of complicated materials, it could not finish the calculation within reasonable time because the program must check all possible arrangements. We here propose a new method based on the combination of the Monte Carlo method and the R-factor method which can be applied to a crystal structure with several independent atoms. This program makes crystal structure models from XRD data, cell constants, a space group, a chemical formula, and a Z-number in a reasonable amount of time using a personal computer.
2 How to construct structure models
Indexed powder diffraction data, from which cell constants are calculated, are indispensable to start crystal structure analysis. Candidates of the space group are narrowed down to several groups by cell constants and extinction of diffraction. Whenever available, information about the symmetry of the diffraction pattern from TEM is useful. A chemical formula and specific gravity lead to a number of formulae in a unit cell (Z-number). Optimizing isotropic temperature factors is not necessary because intensities are not significantly affected by temperature factors. What is necessary is to find the correct positions of independent atoms in a unit cell. Our proposed method makes structure models as follows. First, the program arranges atomic coordinates in an asymmetric unit at random and calculates the theoretical X-ray powder diffraction pattern on the basis of the space group, the cell constants, and the isotropic temperature factors (B=1.0). Then, the program calculates the R-factor of this model from the theoretical and the observed X-ray diffraction data. Based on the R-factors, the structure models are selected and stored. In the calculation process, the following points should be considered.
2. 1 Axis setting
In a tetragonal or a hexagonal system, for example, c-axes must be 4-fold or 6-fold, respectively, and are uniquely determined from powder diffraction data. However, in some cases, the direction of the unit cell axes of an orthorhombic system is not determined uniquely. In this case, one axis is named in three ways as a-, b-, or c-axis and six cell settings are possible. If a space group has glide planes, a distinction must be observed in specific directions. For example, forsterite, whose space group is Pnma, shows the following extinction, viz. (1)0kl:k+l=2n, (2)hk0:h=2n, (3)h00:h=2n, (4)0k0:k=2n, and (5)00l:l=2n. The observed peak of d=3.880A, indexed as 210 from the cell constants a=10.195, b=5.981, and c=4.756, satisfies the above-mentioned extinction law. If we indexed by other cell constants, a=4.756, b=5.981, c=10.195, the index of the same diffraction peak would become 021, which does not satisfy the extinction law, and the calculated intensity of this peak would be zero. In this case, it is easy to eliminate wrong axis settings. However, when it is not possible to determine the correct axis setting by the extinction law, all possible arrangements must be tried.
2. 2 Wyckoff position
If there are many probable Wyckoff positions for one atom, one position must be selected from all candidates. Let us take forsterite as an example: it has the formula, Mg2SiO4, its Z-number is 4, and it belongs to space group Pnma. There are eight magnesium (Mg) atoms, four silicon (Si) atoms, and sixteen oxygen (O) atoms in a unit cell. Wyckoff positions of Pnma are 4a, 4b, 4c, and 8d [2]. As there are eight Mg atoms in a unit cell, Mg atoms make it possible to locate two different Wyckoff positions of multiplicity 4 (described as 4+4) or one 8d(8) position. Si atoms must be located at the positions of multiplicity 4(4). Oxygen atoms must be located by combinations such as (8+8), (4+4+8), or (4+4+4+4). The total number of combinations is 2×1×3=6 sets. All these combinations must be checked.
2. 3 Asymmetric unit
The search area must be restricted to an asymmetric unit, and positions of all other symmetrically dependent atoms are calculated by symmetry operations. Sometimes, a pair of models brought into coincidence by translation, rotation, or reflection to the other is found. Two models which are related by translation share the same structure with a different origin. When the space group only has the symmetry operation of the first kind, a pair of models related by mirror or inverse is produced. They are an enantiomorph of the other. Restricting the search area to an asymmetric unit of the Chesire group is effective to reduce the total calculation time and eliminate duplicates[3].
2. 4 Discrimination function
Diffraction intensities mainly depend on atomic coordinates. When the number of diffraction peaks is not enough in comparison to the number of atomic coordinates which we can move as variables, the obtained results frequently converge to a local minimum. Many peaks overlap in powder data, and it is not easy to increase the observed diffraction peaks. We introduced a discriminant to avoid falling to a local minimum. The worst structure models show unrealistic atomic arrangements such as improper localization of cations, unreasonable coordination numbers, or heavy distortion in coordination polyhedral. Using the following criteria, incorrect models are eliminated: (1) Pauling's 1st rule, which states that the inter-atomic distances must be larger than the sum of each atomic radius, must be applied; (2) Crystal lattice energy must be reasonably small.
2. 5 Calculation process
A structure model-assembly program was then built taking the above points into account. After users indicate the possible Wyckoff position arrangements, the program searches the suitable structure model automatically by the following process:
[preparation]
(1) Produce all possible indexes and sort them by d-value;
(2) Calculate the multiplicity of diffraction and the Lp factors of each index;
[1st stage] Search in an asymmetric unit
(3) Choose Wyckoff positions for each independent atom at random;
(4) Set the variable atomic coordinates by a random number;
If the inter-atomic distances are larger than the sum of each atomic radius, the model is accepted;
(5) Calculate the theoretical XRD pattern and R-factor;
(6) Sort the obtained models by the R-factor in small order and store the top 300 models;
(7) When the R-factor becomes smaller than a value fixed in advance, the process proceeds to the 2nd stage;
[2nd stage] Search the atomic position in a restricted area.
(8) Select one structural model made in the first stage and move each atom around the initial positions at random. If the R-factor becomes smaller than that of the initial model, the newly obtained model is adopted;
(9) Repeat the above calculation and, if the R-factors converge, proceed to the next stage;
[3rd stage]
(10) Calculate the lattice energy and eliminate incorrect structural models;
If necessary, repeat the above cycle two or three times;
(11) Print out the obtained structure models.
3 Example for calculation
Table 1 Input data for brookite
| Formula | TiO2
|
| Z-number | 8
|
| Space Group | Pbca
|
| Cell constants | a=9.182 | b=5.456 | c=5.143A
|
| Atoms | valence | atomic radius | Wyckoff position
|
| Ti1 | 4 | 0.70 | 8c
|
| O1 | -2 | 1.30 | 8c
|
| O2 | -2 | 1.30 | 8c
|
For X-ray diffraction data used in calculation, see Dobs. and Iobs in Table 2.
Table 2 Obtained structure models for brookite
| R-factor= 0.046
|
| obtained structure | reference structure*
|
| atom | w.p. | x | y | z | x | y | z
|
| Ti | 8c | 0.129 | 0.104 | 0.138 | 0.1290 | 0.0972 | -0.1371
|
| O | 8c | 0.006 | 0.093 | -0.199 | 0.0101 | 0.1486 | 0.1824
|
| O | 8c | 0.237 | 0.161 | 0.461 | 0.2304 | 0.1130 | -0.4629
|
|
|
| Dobs. | Dcal. | Iobs. | Ical. | H | K | L
|
| 3.510 | 3.513 | 100 | 100 | 2 | 1 | 0
|
| 3.470 | 3.466 | 80 | 81 | 1 | 1 | 1
|
| 2.900 | 2.901 | 90 | 90 | 2 | 1 | 1
|
| 2.729 | 2.728 | 4 | 3 | 0 | 2 | 0
|
| 2.476 | 2.476 | 25 | 23 | 1 | 0 | 2
|
| 2.409 | 2.410 | 18 | 18 | 0 | 2 | 1
|
| 2.370 | 2.369 | 6 | 8 | 3 | 1 | 1
|
| 2.344 | 2.345 | 4 | 4 | 2 | 2 | 0
|
| 2.332 | 2.331 | 4 | 3 | 1 | 2 | 1
|
| 2.296 | 2.295 | 5 | 3 | 4 | 0 | 0
|
| 2.254 | 2.255 | 8 | 9 | 1 | 1 | 2
|
| 2.244 | 2.243 | 18 | 18 | 2 | 0 | 2
|
| 2.133 | 2.134 | 16 | 15 | 2 | 2 | 1
|
| 1.969 | 1.969 | 16 | 21 | 3 | 0 | 2
|
| 1.893 | 1.893 | 30 | 30 | 3 | 2 | 1
|
| ----- | 1.871 | --- | 2 | 0 | 2 | 2
|
| 1.851 | 1.852 | 13 | 15 | 3 | 1 | 2
|
*:reference structure is derived from Wyckoff[5]
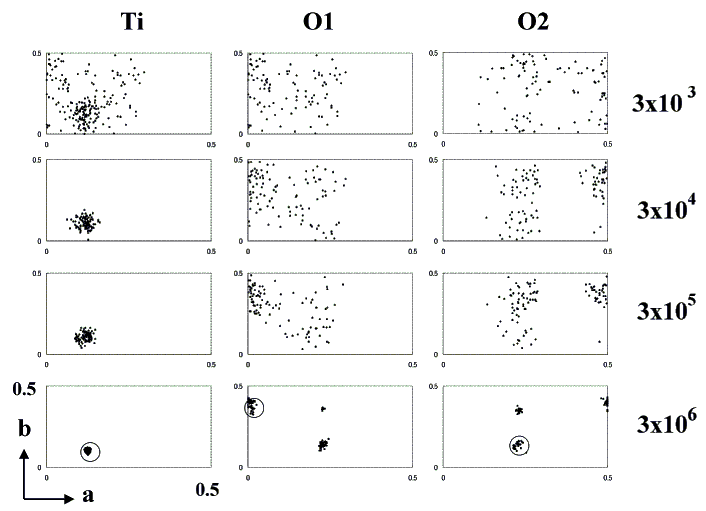
Figure 1. Convergence of atomic coordinates of brookite. Ti, O1 and O2 positions in asymmetric unite of best one hundred models after 3×103, 3×104, 3×105 and 3×106 Monte Carlo trials are projected on (001) plane. All atoms concentrate to each circles in the asymmetric unit which shows the real atomic position.
3. 1 Brookite (TiO2)
The structure model of brookite was produced by the crystal data described in JCPDS Card No. 29-1361[4], including the space group, the chemical formula, the Z-number, and the cell constants (Table 1). The space group of brookite reported in JCPDS Card No. 29-1361, Pcab, was changed to Pbca, the standard lattice setting described in International Tables Vol. A (IT). Cell parameters were changed to a=9.189, b=5.4558, and c=5.1429A. There are eight titanium atoms and sixteen oxygen atoms in a unit cell. As the multiplicity of general position is eight, it is assumed that one independent Ti atom and two independent O atoms exist on 8c positions. In the first stage, 300 models were selected from 600 thousand produced by a random number. The change of the coordinates of independent atoms in an asymmetric unit (0<=x,y,z<=1/2) of the best 100 models was projected on 001 planes (Figure 1). As the number of loops increased, the area in which each atom exists became clear. In the second stage, the search area for the independent atoms was narrowed down to the vicinity of the atoms of the obtained models, and the R-factors were dramatically reduced (Figure 2). The R-factor decreased linearly to the logarithm of the Monte Carlo number. If the search area were not reduced, 6×107 Monte Carlo numbers would be required. This process reduces calculation time dramatically as well (1/30). Eight models giving the best R-factors were obtained. Atoms were situated in mirror symmetry by the (100) plane with x=1/4, the (010) plane with y=1/4, and the (001) plane with Z=1/4. These models were in enantiomorphic relation. Searching all asymmetric units of the space group was not necessary. The Ti atom could be found in the asymmetric units of the Chesire group (0<=x<=1/4, 0<=y<=1/4, 0<=z<=1/4). The finally obtained crystal structural model and the observed and calculated XRD data after 2.58 million loops are listed in Table 2.
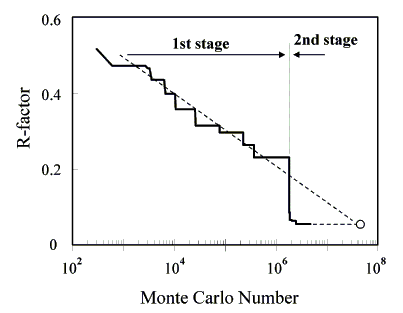
Figure 2. Change of R-factor. R-factor decrease linearly to the logarithm of Monte Carlo number in the first stage and decrease dramatically after the search range was narrowed.
3. 2 Forsterite (Mg2SiO4)
The crystal structure of forsterite was solved from the data of JCPDS 21-1260. The initial data used for the calculation are listed in Table 3. There were 6 possible arrangements of atom positions, as described earlier. The R-factor convergence of 6 arrangements was compared from 30 thousand models, and arrangements of Wyckoff positions (4+4) for Mg and (4+4+8) for O were selected for further calculation because they gave the best R-factor. After 30 million Monte Carlo trials, the program proceeded to the second stage. Although no theoretical parameters were available to indicate the exact timing to start the second stage, this timing was estimated by the experimental parameter of the difference between the R-factors of the top and the 300th model. If the difference became smaller than 0.1, it could be concluded that the calculation converged. In the second stage, the same process mentioned in the case of brookite was applied. In this stage, the R-factor decreased dramatically and reached the real structure model. The used XRD data from JCPDS 21-1260 and the calculated XRD data from the obtained crystal model are listed in Table 4.
Table 3 Input data for forsterite
| Formula | Mg2SiO4
|
| Z-number | 4
|
| Space Group | Pnma
|
| Cell constants | a = 10.195 | b = 5.981 | c = 4.756A
|
| Atoms | valence | atomic radius | Wyckoff position
|
| Mg1 | 2 | 0.40 | 4a 4c
|
| Mg2 | 2 | 0.40 | 4b 4c
|
| Si1 | 4 | 0.40 | 4a 4b 4c
|
| O1 | -2 | 1.30 | 4a 4b 4c
|
| O2 | -2 | 1.30 | 4a 4b 4c
|
| O3 | -2 | 1.30 | 8d
|
For Xray diffraction data used in calculation, see Dobs. and Iobs. in Table 4.
Table 4 Obtained structure model for forsterite
| R-factor= 0.118
|
| obtained structure | reference structure*
|
| atom | w.p. | x | y | z | x | y | z
|
| Mg | 4a | 0 | 0 | 0 | 0 | 0 | 0
|
| Mg | 4c | 0.283 | 0.250 | 0.000 | 0.280 | 0.250 | -0.013
|
| Si | 4c | 0.101 | 0.250 | 0.443 | 0.098 | 0.250 | 0.433
|
| O1 | 4c | 0.086 | 0.250 | 0.783 | 0.092 | 0.250 | 0.790
|
| O2 | 4c | 0.464 | 0.250 | 0.211 | 0.449 | 0.250 | 0.219
|
| O3 | 8d | 0.168 | 0.022 | 0.272 | 0.163 | 0.038 | 0.277
|
|
|
| Dobs. | Dcal. | Iobs. | Ical. | H | K | L
|
| 5.100 | 5.098 | 20 | 20 | 2 | 0 | 0
|
| 4.310 | 4.310 | 1 | 2 | 1 | 0 | 1
|
| 3.880 | 3.880 | 64 | 62 | 2 | 1 | 0
|
| 3.720 | 3.723 | 22 | 14 | 0 | 1 | 1
|
| 3.500 | 3.497 | 15 | 13 | 1 | 1 | 1
|
| 3.480 | 3.477 | 14 | 15 | 2 | 0 | 1
|
| 3.010 | 3.006 | 6 | 4 | 2 | 1 | 1
|
| 2.991 | 2.991 | 18 | 15 | 0 | 2 | 0
|
| 2.764 | 2.765 | 62 | 0 | 3 | 0 | 1
|
| 2.579 | ----- | 1 | -- | | |
|
| 2.509 | 2.510 | 80 | 65 | 3 | 1 | 1
|
| 2.457 | 2.457 | 100 | 100 | 1 | 2 | 1
|
| ----- | 2.378 | -- | 1 | 0 | 0 | 2
|
| 2.344 | 2.345 | 12 | 16 | 4 | 1 | 0
|
| 2.316 | 2.316 | 10 | 6 | 1 | 0 | 2
|
| 2.267 | 2.267 | 44 | 41 | 2 | 2 | 1
|
| 2.246 | 2.245 | 30 | 32 | 3 | 2 | 0
|
| 2.160 | 2.155 | 20 | 20 | 2 | 0 | 2
|
| ----- | 2.103 | -- | 1 | 4 | 1 | 1
|
| 2.030 | 2.027 | 5 | 1 | 2 | 1 | 2
|
*:reference structure is derived from Wyckoff[5]
4 Conclusion
The combination of the Monte Carlo method and the R-factor method can solve simple oxide and silicate structures on the basis of indexed powder diffraction data and chemical formulae. This method is useful for X-ray crystal structural analysis. Atom positions in a unit cell were searched approximately in the first stage and precisely in a restricted area in the second stage. This process, which reduces the total calculation time, can be carried out with a small personal computer. Its most significant advantage is that it does not require preliminary knowledge about the structure. As machine power increases, our method will become more efficient to solve more complex structures.
This work was supported by a grant-in-aid for Scientific Research (Project number, 10640458) from the Ministry of Education, Japan, which is gratefully acknowledged.
References
[ 1] Miura, H., Journal of the Ceramic Society of Japan, 105, 536-540 (1997).
[ 2] International Tables for Crystallography Vol.A, Ed. by Theo Hahn, D.Reidel Publishing Co., Dordrecht (1987).
[ 3] Sakurai, T., A practical Guide for X-ray crystal structure analysis, Syokabo (1983), p144-145.
[ 4] Mineral Powder Diffraction File, JCPDS International Center for Diffraction Data (1985).
[ 5] Crystal Structures, Ed. by Wyckoff, R. W., Interscience, New York (1965).
 Return
Return

 Return
Return