Virtual Device Simulator of Bipolar Photogalvanic Cell
Hidenobu SHIROISHI, Yuuki KABURAGI, Michiko SEO, Takayuki HOSHI, Tomoyo NOMURA, Sumio TOKITA and Masao KANEKO
 Return
Return
1 Introduction
Today, global warming and the rapid decrease in energy resource caused by the large scale consumption of fossil fuel have become serious. Renewable energy resources are attracting a great deal of attention, and solar energy is one of the most promising future energy resources. Although the conventional solar cell is an amorphous silicone type, a new type solar cell developed by Gratzel et al. in 1991 has drawn great attention because of its high cost performance and fairly high energy conversion efficiency [1 - 3]. Only three kinds of efficient photo-energy conversion systems have been known, i.e., p-n junction semiconductors, Gratzel type sensitized solar cells, and photosynthesis by plants. The p-n junction semiconductors can separate electrons and holes efficiently by potential gradient caused by the depletion layer. The reaction center of photosynthesis can separate electrons and holes by utilizing a sensitizer and a series of redox molecules that make a one-way path of electrons.
Although many researches for developing photochemical energy conversion systems have been carried out during the last two decades by utilizing a Langmuir-Blodgett film [5 - 7], SAM [8], a polymer film with dispersed functional molecules [9 - 11] and so on, no efficient system has been developed except semiconductor systems as mentioned above. It is now important to know if an efficient system can be constructed without semiconductor.
The calculation speed of a personal computer is getting faster, and its main memory and a storage device are becoming larger every year. Numerical simulation on a small scale can be done with the computer. Virtual devices on the computer are used for developing actual new devices in various industrial fields. Such a device on the computer would be also useful in the chemistry field.
In the present study, we have developed a virtual device of a bipolar photogalvanic cell which consists of two layers with dispersed functional molecules, and studied whether such a device is able to function as an efficient photo-energy conversion system.
2 Design of Virtual Bipolar Photogalvanic Cell
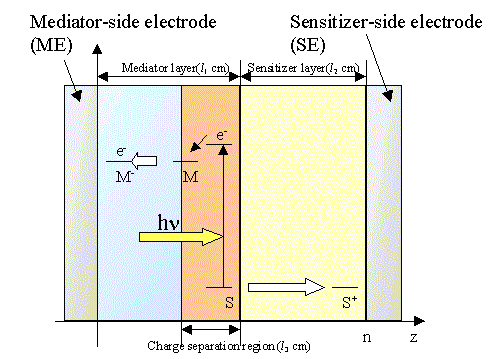
Figure 1. Schematic representation of the bipolar photogalvanic cell to indicate the electron energy level in the different phases.
Figure 1 shows a schematic illustration of the energy levels of a bipolar photogalvanic cell. The cell consists of two layers of different nature with dispersed functional molecules; i.e., polyanion and polycation polymer layers, polyanion polymer and solution layers, and polycation polymer and solution layers. The mediator layer involves vacancies or cracks to which sensitizer molecules are accessible to form a charge separation region. It is assumed that the sensitizer cannot penetrate the mediator layer beyond the charge separation layer. The mediator cannot also penetrate the sensitizer layer.
2. 1 Charge Separation Region
We assumed the following reactions in the charge separation region:
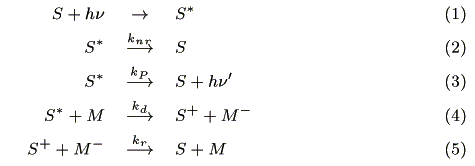
where S is a sensitizer, knr (s-1) is a radiationless deactivation rate constant, kp (s-1) is a luminescence rate constant, kd (mol-1cm3s-1) is a charge separation rate constant where M is an acceptor, and kr (mol-1cm3s-1) is a recombination rate constant.
Assuming that incident photons are absorbed by a micro volume (1cm × 1cm × Dz), the decrease in the number of photons follows the Lambert-Beer law:
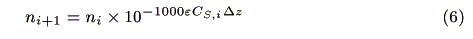
where ni (s-1) and ni+1 (s-1) are the number of incident photons at z = i and transmitted photons at z = i + 1, respectively, CS,i (mol cm-3) is the concentration of the ground state sensitizer, e (mol-1dm3cm-1) is a molar absorption coefficient. The increment of the excited state of the sensitizer in the microvolume, DCS*,i(mol cm-3s-1) is expressed by the following equation:
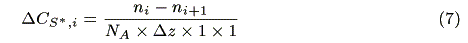
where NA is the Avogadro's number. The concentration of the sensitizer in the excited state, CS*,i (mol cm-3) is represented by a steady state approximation as:
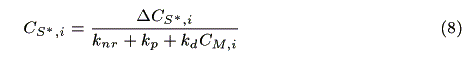
where CM,i (mol cm-3) is the concentration of the mediator at z = i. The mass balance of oxidized sensitizer (S+) in a micro volume (1 cm × 1 cm × Dz cm) is expressed as:
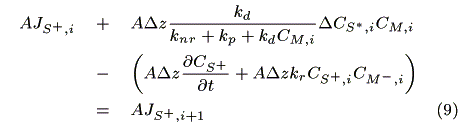
where A (cm2) is a cross section of the electrode, JS+,i (mol cm-2s-1) is a molar flux of S+, CM-,i is the concentration of the reduced mediator. We obtain eq. 10 by dividing both sides of eq. 9 by ADz and substituting Fick's law in it.
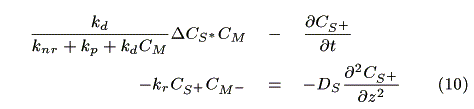
where DS (cm2s-1) is a diffusion coefficient of the sensitizer. It is assumed that DS  DS+.
DS+.
2. 2 Mediator Layer and Sensitizer Layer
In the mediator layer, M- is not generated, and is not recombined with S+. Assuming that DM  DM-, the diffusion equation of M- can be expressed as:
DM-, the diffusion equation of M- can be expressed as:

In the same manner of M-, the diffusion equation of S+ is expressed as:

2. 3 Estimation of Short-circuit Photocurrent
Assuming that the diffusion of redox species is the rate-determining step on the electrodes, each maximum electrode current is expressed by the following equation based on Fick's law [12]:
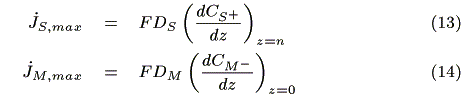
where F (C mol-1) is the Faraday constant, jS, max (A) and jM, max (A) are the maximum electrode currents at SE and ME, respectively. In the simulation, the smaller electrode current based on either eq. 13 or 14 is adopted as the actual current. We obtain the concentration of redox species on the electrodes in each case as follows.
I) In the case of jS, max > jM, max
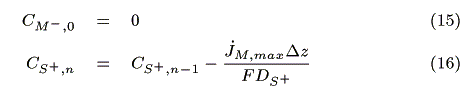
II) In the case of jM, max > jS, max
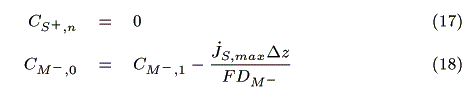
2. 4 Division of Sensitizer Layer and Mediator Layer
Each layer was given the half division number in case the thickness of one layer is substantially different from that of the other layer.
2. 5 Calculations
Each differential equation was solved by the calculus of finite differences.
3 Implementation
We used a PC-9821 machine (NEC) in which the Microsoft Visual Basic version 6(SP3) was installed for developing the virtual photogalvanic cell. The program was tested with Windows 95, 98, Me and 2000 installed in IBM/PC-AT compatibles.
4 Experimental
The following actual device was analyzed using the virtual device.
4. 1 Materials
Tris(2,2'-bipyridine)ruthenium(II) chloride (Ru(bpy)32+) was purchased from Aldrich Chemical Co. Inc. An indium tin oxide glass (ITO) with 10Wcm-2 resistivity was purchased from Kinoene Kogaku Co. Ltd. Potassium haxacyanoferrate(III) and iron(III) nitrate were purchased from Kanto Chemical Co. Inc.
4. 2 Cell Fabrication
Figure 2 shows the configuration of the sandwich type photogalvanic cell. The same volume of a 10mmol dm-3 potassium haxacyanoferrate(III) and a 10mmol dm-3 iron(III) nitrate aqueous solution were mixed to obtain a Berlin Brown solution [13]. The Prussian Blue (abbreviated to PB, Fe4[Fe(CN6)]3) was deposited electrochemically in the Berlin Brown solution at 0.6V vs. Ag|AgCl on an ITO electrode covered with a spacer (thickness, 65 mm) with a window (5mm × 5mm) to obtain PB coated ITO (ITO|PB). A Ru(bpy)32+ aqueous solution was cast onto the ITO|PB electrode, and the ITO|PB and a counter ITO electrode were fastened with a clip to fabricate a sandwich type cell, ITO|PB|Ru(bpy)32+|ITO.
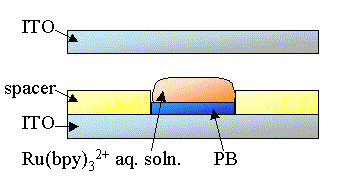
Figure 2. Configuration of a bipolar photogalvanic cell.
4. 3 Measurements
The cell was irradiated with a tungsten-halogen lamp through a cut-off filter of Toshiba L-42 from the ITO|PB electrode side. The light intensity was 94mW/cm2. Visible absorption spectra were measured by a spectrophotometer (Shimadzu, Multispec-1500). The monochromatic light was obtained with a monochrometer equipped with L-37. The incident light intensity was measured with an irradiation intensity meter (type CA1 from Kipp & Zonen).
5 Results and Discussion
5. 1 Simulation of Bipolar Photogalvanic Cell
Figure 3 shows the simulated short-circuit photocurrent induced by switching on and off the irradiation using the virtual photogalvanic cell at various combinations of kd and kr, for which the parameters are shown in Table 1. Although similar steady-state photocurrents can be obtained using various combinations of the charge separation and the recombination rate constants, it takes various times to obtain a steady-state photocurrent depending on the parameters. This contrariwise indicates that the charge separation and the recombination rate constants can be estimated by the photocurrent response of an actual device. The simulated short-circuit photocurrent responses at various thicknesses of layers are shown in Figure 4. When the charge separation region expands over the whole mediator layer, an increase in the thickness of the mediator layer reduces the steady-state photocurrent (Cell A and B).
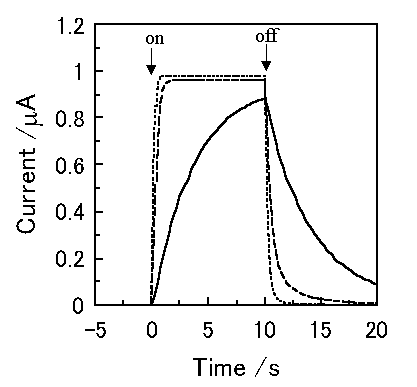
Figure 3. Photocurrent changes induced by switching on and off the irradiation using a virtual photogalvanic cell. -, kd = 5 mol-1cm3s-1, kr = 1 × 105 mol-1cm3s-1; ---, kd = 50 mol-1cm3s-1, kr = 1 × 107 mol-1cm3s-1; ..., kd = 500 mol-1cm3s-1, kr = 1.5 × 109 mol-1cm3s-1.
Table 1. Parameters for the simulation.
| DM /10-11cm2s-1 | 5.0 |
| CM /10-3mol cm-3 | 6.2 |
| DS /10-7cm2s-1 | 1.0 |
| CS /10-5mol cm-3 | 1.0 |
| l1 /10-5cm | 2.5 |
| l2 /10-5cm | 10.0 |
| l3 /10-5cm | 2.0 |
| Intensity /mW | 30.0 |
| Wavelength /nm | 450.0 |
| kP /105s-1 | 7.0 |
| knr /106s-1 | 1.0 |
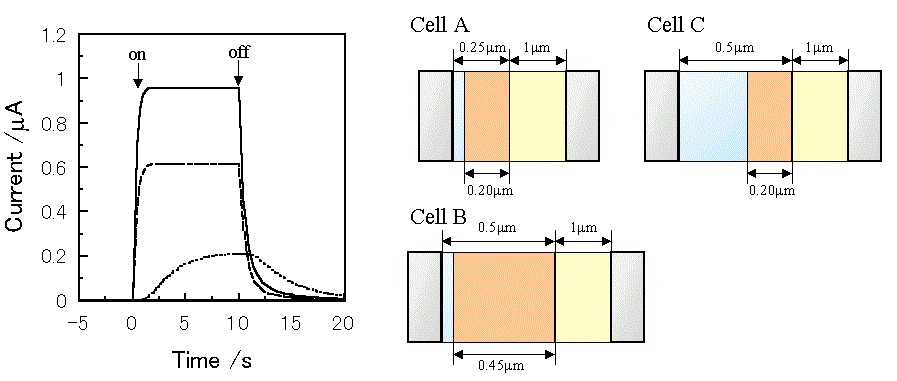
Figure 4. Photocurrent changes induced by switching on and off the irradiation using a virtual photogalvanic cell. -, Cell A;---, Cell B; ..., Cell C. The parameters for the simulation are the same as those in Table 1 except for the thickness of layers. kd = 50 mol-1cm3s-1, kr = 1 ×107 mol-1cm3s-1.
On the other hand, when the sensitizer cannot penetrate into the internal region of the mediator layer, the increase in the mediator layer thickness decreases the steady-state photocurrent, and it takes a longer time to reach the steady-state photocurrent (Cell A and C). This means that the thickness of the charge separation layer can be estimated by measuring photocurrent responses at various thicknesses of the mediator layer using an actual device.
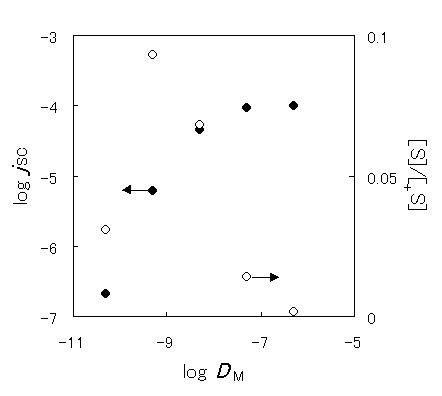
Figure 5. Dependence of the short-circuit photocurrent on the diffusion coefficient of the mediator ( ) and dependence of the fraction of oxidized sensitizer on the apparent diffusion coefficient (
) and dependence of the fraction of oxidized sensitizer on the apparent diffusion coefficient ( ).
).
Figure 5 shows the simulated dependence of the short-circuit photocurrent (JSC) in a steady state on the diffusion coefficient of the mediator (DM) under the conditions where the sensitizer-side is not the rate-determining step. Table 2 shows the parameters for the simulation. JSC increases with the diffusion coefficient, reaching a plateau above DM = 1 × 10-7cm2s-1, whereas the fraction of the oxidized sensitizer increased with the DM at low diffusion coefficients, a maximum value was exhibited around 1 × 10-9cm2s-1 and then it decreased with the diffusion coefficient. It is indicated that not only the diffusion coefficient but also the charge separation efficiency must be improved to advance the performance of the device.
Table 2. Parameters for the simulation.
| CM /10-3mol cm-3 | 6.2 |
| DS /10-7cm2s-1 | 1.0 |
| CS /10-5mol cm-3 | 1.0 |
| l1 /10-5cm | 2.5 |
| l2 /10-5cm | 10.0 |
| l3 /10-5cm | 0.0 |
| kd /mol-1cm3s-1 | 50.0 |
| kr / 107mol-1cm3s-1 | 1.0 |
| Intensity /mW | 30.0 |
| Wavelength /nm | 450.0 |
| kP /105s-1 | 7.0 |
| knr /106s-1 | 1.0 |
5. 2 Application to an actual system
Figure 6 shows the short-circuit photocurrent induced by irradiation on the ITO|PB|Ru(bpy)32+|ITO. Anodic photocurrent was obtained with respect to the ITO|PB electrode. The photocurrent reached 2.3 mA/cm2, although this value was not optimized.
The action spectrum for the short-circuit photocurrent is shown in Figure 7. The action spectrum agreed with the absorption spectrum of [Ru(bpy)3]2+ indicating that the photocurrent was induced by the excitation of the Ru complex. The most probable process is electron transfer from the [Ru(bpy)3]2+* to PB as reported earlier by our group [14].
PB has the two redox couples shown below [15, 16]:

The injected electrons have a potential of around 0.17V vs. Ag|AgCl as estimated from the formal potential of eq. 19. Possible reactions at the cathode are either eq. 21 or 22:
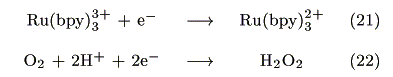
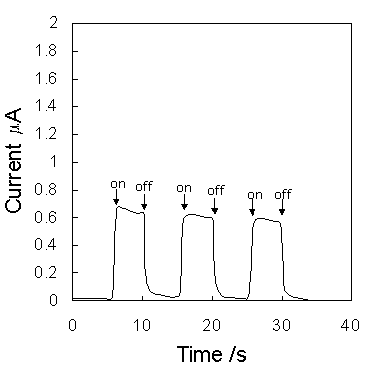
Figure 6. Current changes induced by switching on and off the irradiation on the cell (0.25cm2).
However, eq. 22 is negligible because dioxygen was reduced below -0.2V vs. Ag|AgCl under this condition (Figure 8). Since the open-circuit voltage was small (0.15V vs. Ag|AgCl), a possible mechanism for the present photogalvanic cell would be expressed as:
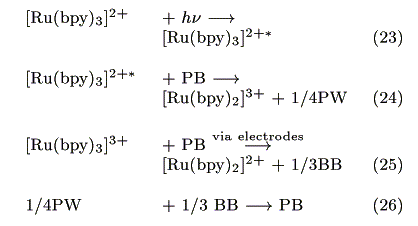
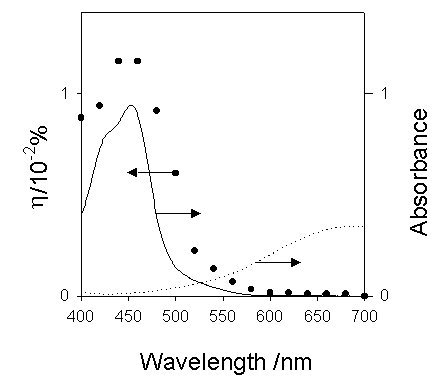
Figure 7. Action spectrum for the short-circuit photocurrent and absorption spectra of Ru(bpy)32+ (-) and Prussian Blue (---).
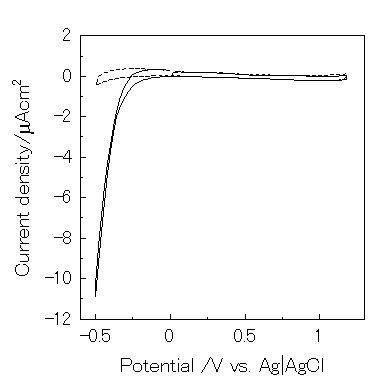
Figure 8. Cyclic voltammogram of ITO electrode in 0.1M KNO3 (pH2) using three electrodes system. Scan rate is 5 mV/s. -, under air; ---, under Ar.
Table 3. Properties of the ITO|PB|Ru(bpy)32+|ITO.
| DM /10-11cm2s-1 | 4.0 |
| CM /10-3mol cm-3 | 6.2 |
| DS /10-6cm2s-1 | 6.0 |
| CS /10-5mol cm-3 | 1.0 |
| l1 /10-5cm | 0.4 |
| l2 /10-5cm | 0.4 |
| l3 /10-4cm | 65.0 |
| kP /105s-1 | 7.0 |
| knr /106s-1 | 1.0 |
| VOC /mV | 118.0 |
| JSC /mAcm-2 | 2.3 |
| Fill Factor /% | 20.5 |
Table 3 shows the properties of the photogalvanic cell as obtained from the experimental results and the simulation. The apparent diffusion coefficients were estimated using Cottrell's equation, and the phosphorescence rate constant (kp) and non-radiative rate constant (knr) were calculated using the quantum efficiency of the phosphorescence (f = 0.042)[17]. The charge separation and the recombination rate constants were estimated from the current response induced by switching on and off using the virtual device, as 5 × 102 mol-1cm3s-1 and 6 × 109 mol-1cm3s-1, respectively.
6 Conclusion
It was indicated that improvement of both the diffusion coefficient of electrons and charge separation efficiency is needed to advance the performance of a bipolar photogalvanic cell. An actual bipolar photogalvanic cell was developed using [Ru(bpy)32+] and Prussian Blue. It was shown that electrons were transferred from [Ru(bpy)32+*] to Prussian Blue. The charge separation and the recombination rate constants were estimated, using the virtual device, as 5 × 102 mol-1cm3s-1 and 6 × 109 mol-1cm3s-1, respectively.
This work was partly supported by a Sasakawa Scientific Research Grant from the Japan Science Society.
References
[ 1] B. O'Regan, M. Gratzel, Nature, 353, 737 (1991).
[ 2] A. Hagfeldt, M. Gratzel, Chem. Rev., 95, 49 (1995).
[ 3] T. Yoshida, K. Yamaguchi, T. Kazitani, T. Sugiura, H. Minoura, J. Electroanal. Chem., 473, 209 (1999).
[ 4] P. Peumans, V. Bulovic, and S. R. Forrest, Appl. Phys. Lett., 76, 2650 (2000).
[ 5] A. Desormeaux, R. M. Leblanc, J. Phys. Chem., 97, 6670 (1993).
[ 6] M. Yoneyama, A. Fujii, S. Maeda, T. Murayama, Appl. Phys. Lett., 58, 2381 (1991).
[ 7] M. Fujihira, K. Nishiyama, H. Yamada, Thin Solid Films, 132, 77 (1985).
[ 8] H. Imahori, T. Azuma, Y. Sakata, Chemical communications, 557 (1999).
[ 9] G.-J. Yao, T. Onikubo, M. Kaneko, Electrochim. Acta, 38, 1093-1096 (1993).
[10] K. Yamada, N. Kobayashi, K. Ikeda, R. Hirohashi, M. Kaneko, Jpn. J. Appl. Phys., 33, L544-L546 (1994).
[11] X.-Y. Yi, L.-Z. Wu, C.-H. Tung, J. Phys. Chem., 104, 9468 (2000).
[12] A. Fujishima, M. Aizawa, T. Inoue, Denkikagakusouteihou, Gihoudou Syuppan Co., Ltd. (1984).
[13] T. Abe, H. Shiroishi, K. Kinoshita, M. Kaneko, Mocromol. Symp., 131, 81-86 (1998).
[14] M. Kaneko, S. Teratani, K. Harashima, J. Electroanal. Chem., 325, 325-332 (1992).
[15] K. Itaya, T. Ataka, S. Toshima, and T. Shinohara, J. Phys. Chem., 86, 2415 (1982).
[16] K. Itaya, I. Uchida, V.D. Neff, Acc. Chem. Res., 19, 162 (1986).
[17] J.V-. Houten, R.J. Watts, J. Am. Chem. Soc., 98, 4853 (1976).
 Return
Return

 Return
Return
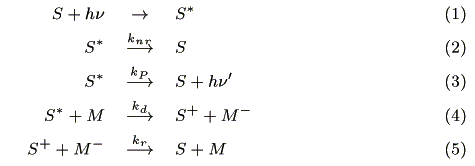
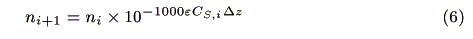
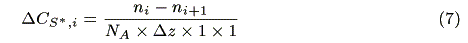
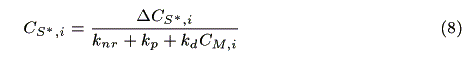
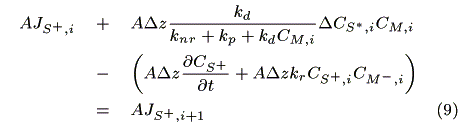
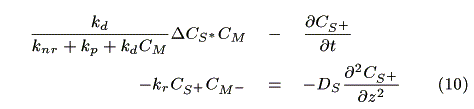
 DS+.
DS+. DM-, the diffusion equation of M- can be expressed as:
DM-, the diffusion equation of M- can be expressed as: 

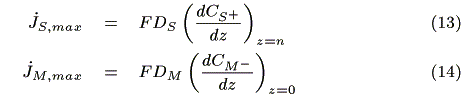
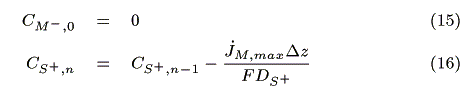
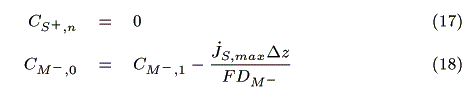




 ) and dependence of the fraction of oxidized sensitizer on the apparent diffusion coefficient (
) and dependence of the fraction of oxidized sensitizer on the apparent diffusion coefficient ( ).
).
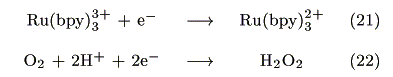

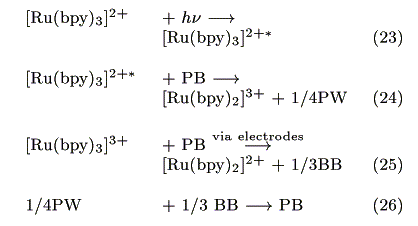


 Return
Return