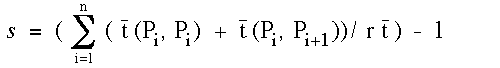(1)
Return
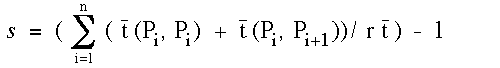(1)
where t(Pi, Pj) stands for a mean travelling time for i
j or a mean
binding time for i = j regarding the points of Pi and Pj, r is the ratio
of the area of a local sphere to that of a unit sphere, n is the number of
binding sites and t is an average unit-sphere-passing-through time in
the medium of interest. P0 and Pn+1 equal Pin, entrance point, and Pout,
exit point, respectively. It is evident that if there is no bonding
between A and L at Pi, t(Pi, Pi) = 0 (perfect reflection) and if, in
addition, a ligand is thrown back by a single contact with an anti-ligand
at P1 ( a center of a local unit sphere) as shown in Fig.1b, s = 0 (no
stickiness).
Originally, stickiness is defined for a local interaction just as
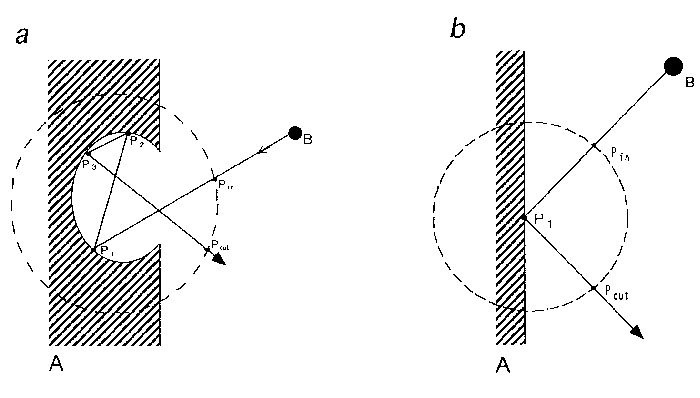
Fig. 1. Definition of stickiness.
(a) Stickiness is defined, as described in the text, through
statistical ensemble of the residence times of a ligand
(symbolized as B) in the inner and the outer regions of a unit
sphere (broken-line circle) fixed in an anti-ligand (i.e.,
macromolecule) symbolized as A. In the inner part of a unit
circle, the ligand is in the state of either binding at the
points such as P1, P2 and P3 or travelling between those
points and the residence time can be obtained from the times
at Pin, entrance into the sphere, and Pout, exit out of the
sphere. (b) Zero stickiness. The symbols are the same as
those denoted in Fig.1a. If no binding at P1 just as perfect
reflection, stickiness is reduced to zero (see Eq.1). Free
travelling in the medium is also zero stickiness by
definition.
described above. However, it can be expanded to a global one by the following formulation:
(2)
where sg is the global stickiness of a pertinent anti-ligand molecule to
a ligand and N is the total number of local spheres. We would like to
treat this general stickiness in a more detailed manner elsewhere, which
must have some relation to the equilibrium constant of binding and has an
analogous nature of the frequency factor appearing in kinetic theory.
In this paper, we want to lead it to a tool for describing DNA-DNA
interactions where an oligonucleotide is a ligand whereas a macromolecule
DNA (often a template DNA) is an anti-ligand. Since it is difficult to
define a local sphere exactly ( 3-D solution structures of DNA are not so
well-known), we have to introduce some approximation for it. A primary
way to substitute for stickiness is to use an equilibrium constant of
binding or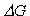 
at a certain site of a template DNA, and we term it
pseudostickiness. It can be so rationalized that since in Eq.1, t(Pi, Pi),
mean staying time, is generally far greater than t(Pi, Pi+1), mean
travelling time, the major factors that govern the value of stickiness, s,
are staying times and by that the staying time has a close relation to an
equilibrium constant of binding, which is the ratio of association to
dissociation kinetic constant and is far greater than unity. In other
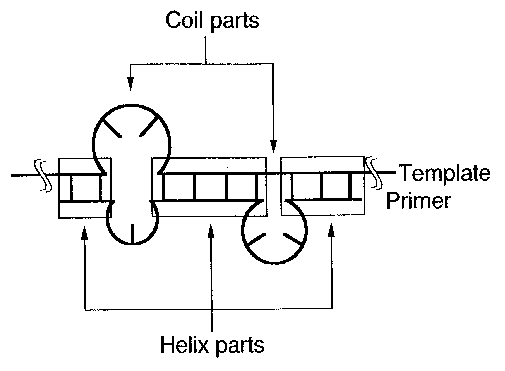
Fig. 2. Calculation of binding free energies as a substitution
of stickiness for a DNA-DNA system. A binding free energy
between a template (anti-ligand) and a primer (ligand) in a
particular conformation at a certain local site of template
DNA is computed by way of the conventional method based on the
thermodynamical parameters for helix stability and non-helix
(called as 'coiled part' in the figure) stability (see
Ref.5). All possible structures conformed to the constraints
are subjected to the calculation of their binding free
energies by computer and those structures which are more
stable than a threshold stability ( 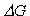in Table I) are picked
up together with their free energies and the site-
informations. The free energy values thus obtained are used as
a substitution of stickiness or pseudostickiness at the site.
As shown in the figure, the coiled parts consist of both bulge
and internal loops, this being taken into consideration during
their free energy calculation.
words, the greater the binding constant, the more the stickiness.
Secondly, we think that calculation time for searching stable
structures between a template and a primer along the sequence of a
template is a good candidate for emulating stickiness since it includes
similar processes2) with attaching-and-detaching in the phenomenon defined
above: the algorithm allows the intensive calculation along the region
which conforms to the given requirements as shown in Table 1 and it leads
to long local residence (long calculation times) in calculating
stabilities of a DNA complex between a template and a primer along the
template DNA sequence. The local residence time for calculation will
become longer as the concentration of stable structures becomes higher in
a limited region. Thus, the calculation time will be roughly proportional
to the stickiness and can be another pseudostickiness. In the following
section (RESULTS AND DISCUSSION), we will use 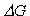-derived pseudostickiness
rather than the calculation time-derived one.
Table I. Constraints imposed for searching stable structures
and the parameters used in the program.
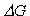was derived from
a PCR analysis program, PCRAna, which was made for searching stable and
semi-stable hybrid structures between a template DNA and an
oligonucleotide and then applied to working out possible PCR products2).
The essential scheme for calculating the stability of a hybrid structure
is depicted in Fig.2. The thermodynamic parameters used were those of
Salser5), which were obtained for RNA but are known to be still usable for
DNA6). The constraints imposed on hybrid structures are listed in Table I.
Pseudostickiness expressed in terms of binding constant, 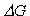, was directly
used just as it was calculated by a computer without any transformations.
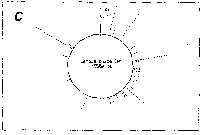
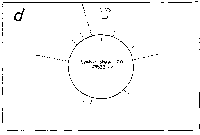
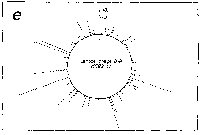
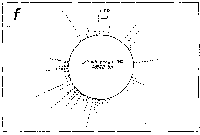
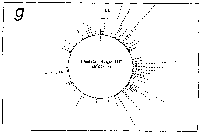
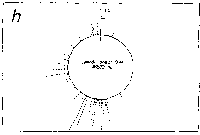
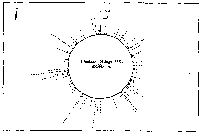
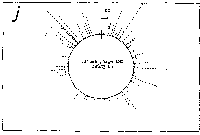
Fig. 3. Pseudostickiness maps of the systems of homo- or co-
polymeric oligonucleotides and lambda DNA. The
oligonucleotides used were (a) d(ApApApApApApApApApApApA) or
d(A)12 in abbreviation (hereafter, similar molecules are shown
in this form), (b) d(T)12, (c) d(C)12, (d) d(G)12, (e) d(GT)6,
(f) d(GA)6, (g) d(GC)6, (h) d(AT)6, (i) d(AC)6 and (j) d(TC)6
whereas the template was lambda DNA throughout. Bars were
stacked at the 5'-end point for each hundred-nucleotide window
sequence in proportion to the number of structures picked up
within the corresponding region. The arrows indicate the
origin in the lambda DNA map and the numbering proceeds
clockwise (see Fig.4).
sequence are shown in Fig.3. Each ligand is shown to have characteristic preferential bindings or pseudostickiness to lambda DNA. From a viewpoint of genome structure, these results can be compared to those obtained with G+C content analysis and DNA stability analysis, which had been done by Wada and Suyama8). Those sticky regions depicted in Fig.3a are (A+T)- rich and also thermodynamically less stable regions according to their results, which are quite natural. These regions are especially remarkable because they fall on unique sites in lambda genome DNA: the left and the
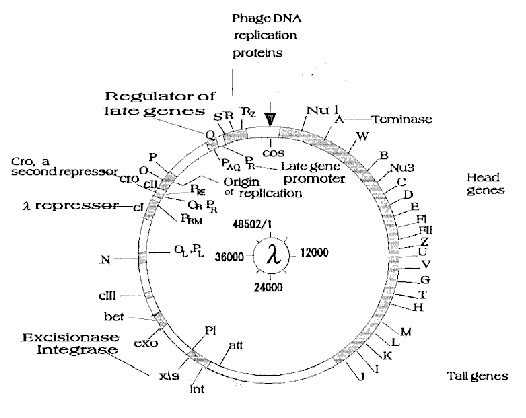
Fig. 4. A genetic map of lambda DNA. The genes were assigned
on lambda DNA together with a brief description of their
function. The starting point of the map (cos site) is
indicated by an arrow and the direction of numbering is the
same (clockwise) as in Fig.3.
right ends of central region (map position; 23000 and 38000, respectively)
as shown in Fig.4. This fact was not so clear in G+C content analysis or
thermal stability analysis8). Furthermore, the ligand of dA12 has local
pseudostickiness solely to central region, which embosses the region
against the remaining ones, although dT12, another (A+T)-rich sequence
have a less clear tendency. As Wada and Suyama pointed out, structural
features disclosed by thermodynamical stability analysis have a stronger
relationship to biological functions than those revealed by G+C content
analysis which does not contain physical meanings8). Since the
pseudostickiness analysis is based on thermodynamics, characteristic
features revealed by it seem to have some connection with biological
functions. It should be noted that (A+T)-rich (or (G+C)-rich) region
analysis could not offer similar results to those provided by the
pseudostickiness analysis with dA12, though it is not possible at present
to predict, a priori, which ligand is effective to reveal such properties.
The other ligands have their characteristic stickiness patterns. This
means that there are as many probes as the diversity of ligand sequence
in order to characterize anti-ligand DNAs such as lambda genome DNA. This
fact is further reinforced by the following experiment.
Single-base-substitution effect--- Five ligands which are single-base-
substitutions of an oligonucleotide, pfM12 (dAGAACGCGCCTG), gave the
pseudostickiness analysis result shown in Fig.5. It evidently indicates
that even a single-base-substitution in a ligand sequence significantly
affects the result of pseudostickiness. This fact is worthy of note since
there are no differences in (G+C)-content between pfM12-8A and pfM12-8T or
among pfM12-8C, pfM12-4C and pfM12-4G and therefore, the differences
detected here are what (G+C)-rich region analysis can never detect.
During these analyses, apparent differences should be translated with
enough caution since the pseudostickiness, which is expressed by a
frequency of bars in Fig.3 and Fig.5, can be changed by a cut-off
parameter ( G) employed. However, we can make a safe comparison among the
data if they are obtained under the same conditions as those given here.
Significance of stickiness--- In this paper, we coined the term,
stickiness, together with its definition. Then, we expanded the concept of
stickiness to a manageable one, pseudostickiness, for DNA-DNA interaction.
The pseudostickiness thus introduced can be regarded as a kind of concept
derived from binding affinity (or binding constant). The most outstanding
difference between pseudostickiness and binding constant is that the
former contains the concept of space while the latter does not. In real
phenomena occurring both in vivo and in vitro, macromolecule interactions
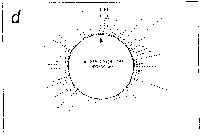
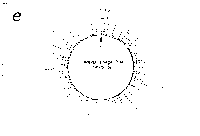
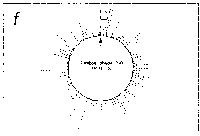
Fig. 5. Oligonucleotide point mutation effect on
pseudostickiness.
Single-base-substituted derivatives of an oligonucleotide
designated pfM12 (dAGAACGCGCCTG) were examined regarding their
pseudostickiness with lambda DNA. The derivatized sequences
are: (a) pfM12 (original), (b) pfM12-8C (i.e., the position
substituted is the 8th and the base to which the original base
(G) was substituted is C, and the following are expressed
likewise), (c) pfM12-4C, (d) pfM12-4G, (e) pfM12-8A and (f)
pfM12-8T. The maps are drawn in the same way as in Fig.3.
are affected by spatial factors such as size, location and orientation,
which is the reason for the necessity of introducing stickiness.
Originally, stickiness is defined for a local event so that it should
be called local stickiness. It implies that there are multiple sticky
sites in a macromolecule which compete to bind a ligand. If one of these
sites is a so-called specific site, i.e., the strongest binding site, the
ligand binding to this site (specific binding) must be influenced
kinetically and thermodynamically by the ligand binding to the rest. This
means that we cannot correctly describe the phenomenon of specific binding
without considering the other non-specific bindings. Therefore, global
stickiness, which denotes the stickiness applied to an entire
macromolecule, becomes a useful property to measure the behavior of a
ligand/anti-ligand system. The conventional approaches which neglect the
global stickiness effect to describe a specific binding are simplistic and
incorrect in this sense. The ratio, in size, of a local region to an
entire macromolecule is crucial in determining whether such a systemic
consideration is required. This is evident especially in an interaction of
a giant DNA and a protein (or an oligonucleotide), where the value of the
ratio is very small. In the usual studies, only the interaction between
the targeted site of a macromolecule and a ligand is considered. However,
we take the remaining regions of a macromolecule into consideration by
means of global stickiness in order to obtain a quantitative prediction
for the behavior of a ligand/macromolecule system. One illustrative
example for this is an interaction between a promoter buried in a big DNA
and an RNA polymerase. Without the information provided by global
stickiness, one will not be able to explain their behavior quantitatively
provided with their dissociation constants and their concentrations in a
cell. In other words, the behavior of a molecule is affected by not only
its direct partner but also its surroundings. Elucidation of this fact
and introduction of a reasonable method to deal with this is the most
essential contribution of this paper to science.
Return