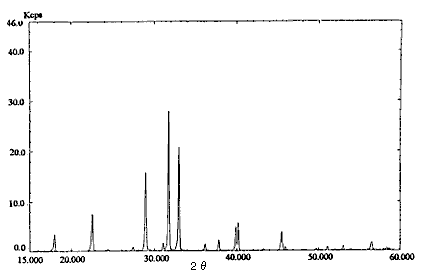
Fig.1 X-ray diffraction pattern
(Ammonium nitrate : Sodium chloride = 1 : 4)
Return
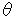) of a specific peak obtained by XRD diffraction method is about 10 %. However, when the integrated intensity of various peaks (2 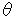) for one sample was used for the determination, the reproducibility was less than 1.0 %. The determination of ammonium nitrate content was calculated by multivariate analysis[2 - 4] such as cluster analysis and principal component analysis (PCA).
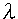= 1.54056 A ) was used for the measurements of the samples. The samples were measured continuously or by an integration method. This was done at 40 kV and 40 mA. The scan speed was 5.00 per min. An NEC PC-9801 RX personal computer was used for the calculation of the data. The language used in the program was Basic. The software of Principal component regression analysis (PCR) and Partial least squares regression analysis (PLS) were used Pirouette (GL Sciences Co., Ltd.).
Fig.1 X-ray diffraction pattern
(Ammonium nitrate : Sodium chloride = 1 : 4)
Pre-treatment of a real sample (dynamite) was as follows. Twenty mL of diethyl ether was added to about 1 g of the sample and organonitro compounds were removed. This operation was repeated twice. The residue was dried and about 0.25 g sodium chloride was added for safety and as an internal standard. These compounds were analyzed by an X-ray diffraction method. The pattern of ammonium nitrate : sodium chloride = 1 : 4 is shown in Fig. 1.
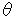= 17.98, 22.48, 28.94, 32.96, 36.14, 37.78, 39.86, 40.16, 51.09 for ammonium nitrate) each divided by 2 normalization factors (2 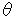= 31.72, 56.50 for sodium chloride) were obtained. The obtained matrix (9 x 18) was used in Quantification IV[5]. Quantification IV is a method for selecting a useful category in multivariate analysis. The eigen vectors were obtained as a result of Quantification IV, and the categories whose eigen vectors were in the range of -0.500 to +0.500 were selected in 18 categories. The categories indicating more than +0.500 or less than -0.500 of the eigen vectors were hardly differentiated or changed at random compared with the variation in ammonium nitrate content. They were not used for the multivariate analysis. At this time, 17 categories were selected. One category was not very good for use in the multivariate analysis. In the quantitative analysis of ammonium nitrate, the 17 categories were also selected for 9 known samples and one unknown sample.
PCSs(1) =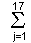
((Uij - 50.000) x F1j ) / D1 . . . . . (1)
where PCSs(1), Uij, F1j and D1 are the first principal component score for the each sample, the reformed deviation value for sample number i, the first principal component and the first eigen value of the first principal component, respectively. If the second eigen value of the second principal component is larger than 1.000, the second PCSs (PCSs(2)) are obtained from equation (2).
PCSs(2) =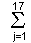((Uij - 50.000) x F2j ) / D2 . . . . . (2)
where PCSs(2), F2j and D2 are the second principal component score for each sample, the second principal component and the second eigen value of the second principal component, respectively.
In the case of the conventional method (calibration curve method), only one peak for both the standard and unknown samples has been used for the determination of ammonium nitrate content, the other peaks have not been used because they were not very good for use in the determination of ammonium nitrate content. Single linear regression is used to derive a relationship between the concentration and the measurement. Also, the calibration curve is prepared only for the measured values for known samples. The determination is carried out by substituting the measured value for the unknown sample for the calibration curve. In PCA, the measured values for unknown and known samples were calculated for the determination of ammonium nitrate content at the same time. The obtained PCSs corresponding to the measurement values of the calibration curve were used for the determination of the ammoniun nitrate content. Therefore, the PCSs of the 9 known samples were changed according to the unknown sample. The determination of ammonium nitrate content by PCA is carried out from the PCSs for each row for the eigen value of > 1.00. If the PCSs for all rows are used for the determination, the calculation becomes more precise than the above but as a result, the calculating time for the PCA becomes very long and the result of the determined value between the PCS for each row eigen value of > 1.00 and the PCS for all rows is almost the same. So we made the determination using the PCS for each row based on an eigen value of >1.00.
The method of determination is shown below.
Chart 1 Example of ammonium nitrate content in dynamite from principal component analysis
Select 17 categories from X-ray diffraction result using Quantification IV
Input data
------------------------------------------------------------------------------------------ Sample Categories No. No. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 ------------------------------------------------------------------------------------------ 1 0 0 1 0 0 0 0 0 5 9 32 12 0 3 5 8 0 2 0 1 1 0 0 0 0 0 8 27 62 75 6 4 19 14 0 3 1 1 4 0 0 2 1 0 24 61 191 203 10 18 74 40 9 4 2 3 6 1 1 2 2 0 58 127 232 271 20 25 70 66 9 5 3 7 11 1 1 3 3 0 94 204 335 375 23 34 96 80 10 6 5 12 25 2 2 7 5 1 101 242 496 691 33 33 134 102 21 7 8 22 34 4 4 13 10 1 117 337 519 749 56 65 204 147 19 8 12 27 57 5 8 17 20 3 204 459 966 1263 82 133 296 348 44 9 28 60 110 7 13 27 30 4 288 611 1126 2326 73 130 280 303 39 10 8 18 33 2 3 11 11 1 133 318 563 529 37 54 197 189 21 ------------------------------------------------------------------------------------------The data are multiplied by 100. Sample number 10 : real unknown sample
----------------------------------------------------------------
Categories Principal component
No. 1 2 3 4 5 6
----------------------------------------------------------------
1 0.957 -0.285 0.016 0.032 -0.022 0.010
2 0.967 -0.246 -0.062 -0.004 -0.029 0.010
3 0.977 -0.208 0.015 0.032 -0.022 0.010
4 0.987 -0.058 -0.093 -0.112 0.049 -0.008
5 0.982 -0.153 0.047 -0.101 0.012 -0.025
6 0.989 -0.068 -0.081 -0.044 -0.059 0.055
7 0.991 -0.072 0.076 -0.053 -0.073 -0.004
8 0.992 -0.075 0.085 -0.013 0.029 0.055
9 0.987 -0.008 -0.019 0.135 0.001 -0.073
10 0.985 0.048 -0.127 0.100 -0.008 -0.050
11 0.989 0.102 0.025 0.093 0.005 -0.007
12 0.970 -0.200 0.039 0.044 0.113 0.006
13 0.949 0.275 -0.096 -0.077 0.085 -0.011
14 0.974 0.171 0.068 -0.096 0.008 -0.071
15 0.950 0.276 -0.112 0.010 -0.058 0.066
16 0.955 0.255 0.111 -0.014 -0.084 -0.036
17 0.948 0.270 0.108 0.070 0.056 0.075
Eigen values 16.116 0.600 0.104 0.089 0.048 0.031
----------------------------------------------------------------
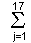(Uij - 50.000) x F1j ) / D1
Principal component score of each sample
-----------------------------------------------------------------------
Sample No. Principal component score NH4NO3/NH4NO3+NaCl
-----------------------------------------------------------------------
1 39.46 0.0922
2 39.96 0.1808
3 42.12 0.3082
4 43.50 0.3985
5 45.47 0.4963
6 48.81 0.6128
7 53.45 0.6962
8 63.37 0.7925
9 71.58 0.9047
Real unknown sample 52.27 ---
-----------------------------------------------------------------------
The PCS1 of the known sample was larger than that of the unknown sample (PCSx) and nearest to it, and another (PCS2) was smaller than that of the unknown sample and nearest to it. The linear relationship was computed from equations (3) and (4).
Table 1 Analytical results (prepared unknown sample)
--------------------------------------------------------
Sample Content of NH4NO3 ( % )
No. PCA PCR PLS CM TV
--------------------------------------------------------
1 18.63 17.82 18.15 21.01 18.08
2 40.14 38.11 38.76 40.13 41.46
3 53.90 55.78 55.40 53.64 55.52
4 69.62 69.58 69.60 63.65 69.62
5 74.75 73.97 73.69 76.59 73.77
6 90.13 88.65 88.87 88.66 90.47
--------------------------------------------------------
PCA:Principal component analysissample No. 3. However, in the case of the conventional method using calibration curves prepared by the category indicating the best correlation coefficient in the seventeen categories mentioned above, reproducibility was about 4.9 % (n = 10). The PCA was the best method in PCA, PCR and PLS. The PCA method is thus suggested to be useful in quantitative analysis by the X-ray diffraction method. Similarly, ammonium nitrate in four real dynamite samples was determined. The results are shown in Table 2.
Table 2 Analytical results for 4 real dynamite samples
-----------------------------------------------
Sample Content of NH4NO3 ( % )
No. PCA PCR PLS CM
-----------------------------------------------
1 67.00 65.54 66.65 72.55
2 70.08 68.42 69.88 66.18
3 77.48 77.31 77.36 82.00
4 78.14 78.29 78.34 80.07
-----------------------------------------------
Return